[¯|¯] Gli zeri della funzione zeta di Riemann sono le singolarità della sua derivata logaritmica
Agosto 6th, 2019 | by Marcello Colozzo |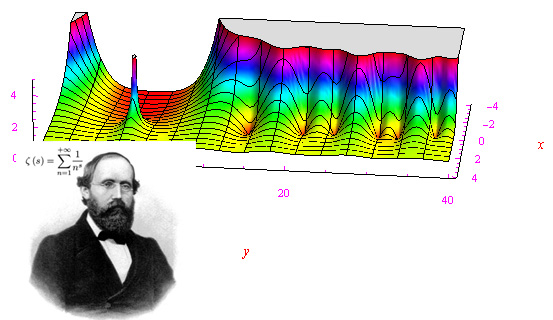
Se z=x+iy è l'usuale variabile complessa, la funzione zeta di Riemann è definita come:

dove il pedice HE denota l'estensione olomorfa i.e. il prolungamento analitico della funzione assegnata. Ricordiamo che la funzione zeta è olomorfa in tutto C tranne nel punto z=1, dove ha un polo semplice:

Si tratta, quindi, di una funzione meromorfa.
La derivata logaritmica è definita come
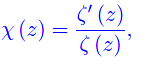
dove l'apice denota l'operazione di derivazione complessa. Riesce
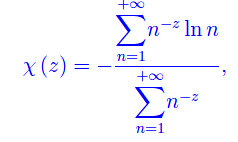
giacchè la derivata prima è ancora una somma (ove converge) di una serie di Dirichlet. Nello specifico, tale serie ha coefficienti cn=-ln(n).
Ciò premesso, dimostriamo il seguente teorema che risolve l'indeterminazione: se z0 è uno zero della funzione zeta e della sua derivata prima, si ha:
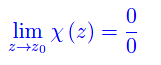
Teorema
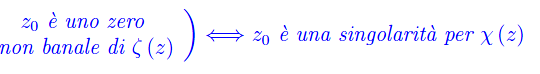
Dim.
Supponiamo che z0 sia uno zero di ordine n. Cioè
Applicando la regola di De L'Hospital:
onde l'asserto.
c.d.d.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: derivata logaritmica, funzione Zeta di Riemann, Singolarità, zeri
Articoli correlati
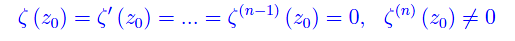
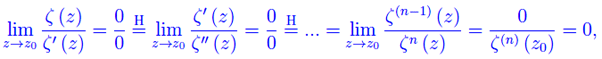


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











