» Esercizi svolti di Matematica e Fisica

[¯|¯] Forza esercitata da una fune. Il concetto di tensione

Novembre 19th, 2018 | by Marcello Colozzo |

Molti problemi di dinamica coinvolgono corpi collegati a carrucole tramite funi. In varie occasioni abbiamo introdotto la nozione di fune inestensibile e di massa trascurabile. In questa lezione cercheremo di rendere più quantitativi tali concetti. In figura

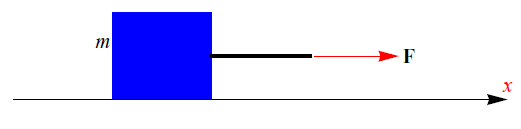
una cassa di massa m è appoggiata su un pavimento privo di attrito. Un operaio trascina la cassa mediante una fune. Sia F la forza applicata dall'operaio al sistema cassa+fune. Denotando con m_fune la massa inerziale di quest'ultima ed invocando il secondo principio della dinamica, si ha:

essendo a l'accelerazione conseguente. Si noti che F non è applicata alla cassa ma all'intero sistema cassa+fune. La forza che agisce sulla cassa è quella esercitata dalla fune:

Definizione
La forza esercitata dalla fune si dice tensione.
Orientando un asse x come nella figura precedente:

Se la fune ha una massa nulla o comunque trascurabile rispetto a m, dal sistema precedente segue:

L'assunto

esprime una condizione ideale, e solo in tal caso è F=T. Un'altra condizione che deve essere verificata è l'assenza di allungamenti, per cui una fune ideale ha massa nulla ed è inestensibile. Per chiarire quest'ultimo concetto, aggiungiamo allo schema precedente una seconda cassa:

Le forze agenti sulla prima cassa:

Per il secondo principio della dinamica:

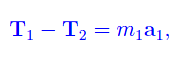
dove a1 è l'accelerazione della prima cassa. L'unica forza che agisce sulla cassa di massa m2 è la tensione T2 esercitata dalla fune 2, onde

essendo a2 l'accelerazione di m2. Eliminando T2 tra le appropriate equazioni

Le due casse hanno accelerazioni diverse, a causa dell'eventuale allungamento della fune 2. Nel caso contrario, cioè se la fune non subisce allungamenti, dovrà essere a1=a2=a, per cui

Applicando il secondo principio della dinamica all'intero sistema:

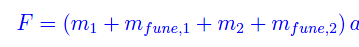
Se le funi hanno massa nulla:

Quindi

Per comprendere l'origine della tensione, supponiamo di avere una fune di lunghezza l con uno dei due capi liberi, mentre l'altro è vincolato:

Il capo libero è sottoposto a una forza di trazione F parallela all'asse della fune tesa. Assumendo un asse x orientato come in figura, eseguiamo una partizione dell'intervallo [0,l], prendendo i seguenti punti equidistanti:

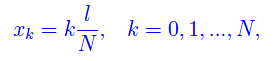
cosicché

Il tratto di fune corrispondente all'intervallo [x_k,x_k+1] esercita una forza di trazione sull'elemento adiacente corrispondente a [x_k-1,x_k], che è parallela e concorde al F, e di modulo che può essere scritto come:

Sommando su tutti gli elementi

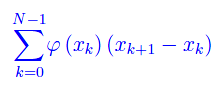
Posto

ed eseguendo l'operazione di passaggio al limite per Δ->0

che è la tensione esercita dalla fune sul vincolo in x=0. La funzione φ(x) è la tensione per unità di lunghezza.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: forza esercitata da una fune, fune ideale, fune inestensibile, tensione

Articoli correlati