[¯|¯] Infinitesimi ed infiniti (Lezione 2)
Febbraio 21st, 2017 | by Marcello Colozzo |
Fig. 1
Un esempio immediato per ciò che riguarda la confrontabilità di infinitesimi è offerto dalla coppia di limiti fondamentali:
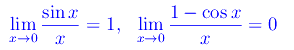
Ne consegue che sin x e x sono (per x->0) infinitesimi dello stesso ordine. Anzi, quando il limite del rapporto è 1, gli infinitesimi si dicono equivalenti:

mentre 1-cos x è un infinitesimo di ordine superiore a x. Tali risultati hanno una notevole interpretazione geometrica che può essere dedotta dall'esame della fig. 1. Dal momento che 2*sin x è la lunghezza della corda PP' sottesa dall'arco di estremi P e P' (la cui lunghezza è 2x), si ha che per x->0 la lunghezza della corda è un infinitesimo dello stesso ordine della lunghezza dell'arco. Diversamente, 1-cos x è la lunghezza della "freccia" QA dell'arco di estremi P e P' e per quanto precede, è un infinitesimo di ordine superiore a x (per x->0). In parole povere, mentre la lunghezza della corda tende a zero con la stessa rapidità con cui si annulla la lunghezza dell'arco, la lunghezza della freccia va a zero più rapidamente.
Tags: infinitesimi, infinitesimi confrontabili, infinitesimi non confrontabili, infiniti, ordine
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











