Somma delle aree e dei perimetri di infiniti quadrati ottenuti per ricorsione

Ottobre 12th, 2021 | by Marcello Colozzo |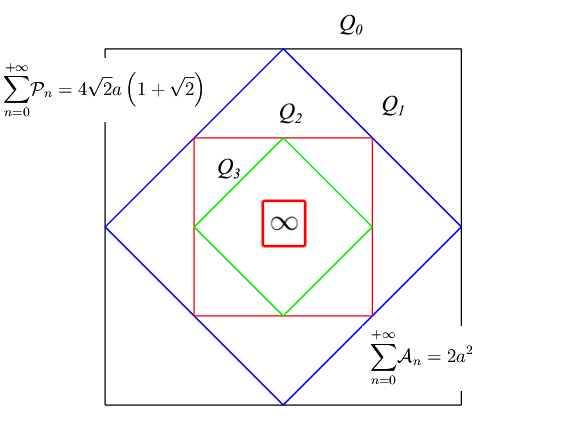

Esercizio tratto (e modificato) dal Gizzetti. La soluzione è nostra.

È dato un quadrato Q₀ di lato a. Si consideri il quadrato Q₁ che ha come vertici i punti medi dei lati di Q₀, poi il quadrato Q₂ avente per vertici i punti medi dei lati di Q1 (fig. 1). Iterando il procedimento si perviene a una successione di quadrati:

ciascuno dei quali è contenuto nel precedente. Dimostrare che la somma dei perimetri e delle aree degli infiniti quadrati ottenuti con tale procedimento ricorsivo, hanno entrambe un valore finito.

Soluzione

È nota la lunghezza a del lato del quadrato Q₀. Guardando la fig. 1 si perviene alla lunghezza del lato di Q₁