Operazione di passaggio al limite. Specificare la topologia dello spazio in cui si lavora
Settembre 29th, 2021 | by Marcello Colozzo |
Premettiamo la seguente proprietà
Proprietà di densità
L'insieme Q dei numeri razionali è denso in R, ossia comunque prendiamo x,y in R con x diverso da y, esistono infiniti numeri razionali compresi tra x e y.
Consideriamo ora la seguente funzione definita in X=Q+ (insieme dei razionali non negativi):
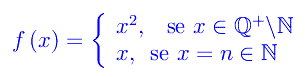
Un assegnato xn=n è di accumulazione per X giacché per la proprietà di densità, in ogni intorno di xn cade almeno un punto (=> infiniti) di X distinto da n. Ciò ci consente di poter applicare la definizione di limite. Nel caso in esame, risulta:
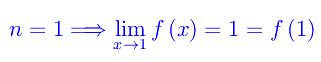
per cui la funzione assegnata è ivi continua. Diversamente:
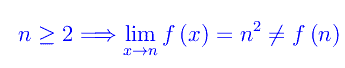
In definitiva:
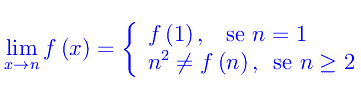



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











