Doppio piano inclinato (meccanica razionale)

Agosto 31st, 2021 | by Marcello Colozzo |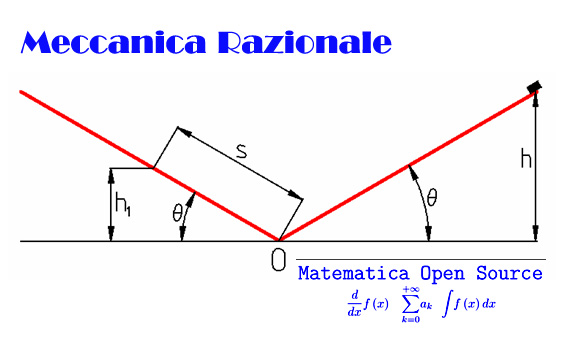

doppio piano inclinato,meccanica razionale
Fig. 1

Esercizi di Meccanica razionale elaborati dell'ing. Giorgio Bertucelli.

Esercizio
La massa dell'esercizio precedente, dopo essere scesa fino al punto O, risale su un piano pure inclinato di θ (fig. 1) e con lo stesso coefficiente di attrito µ. Determinare la massima altezza cui può giungere la massa, sapendo che θ=30° e µ=0.3.

Soluzione
Questa volta il moto sarà uniformemente ritardato con decelerazione


Potremo perciò scrivere velocità e spazio percorso:

La massa si fermerà all'istante

e dopo aver percorso lo spazio

e aver raggiunto l'altezza


Se mancasse l'attrito ovviamente sarebbe h=h1 (teorema di conservazione dell'energia). Sostituendo i valori numerici

No TweetBacks yet. (Be the first to Tweet this post)

Tags: ,

Articoli correlati

Commenta l'esercizio