Esercizio svolto sui limiti (con il Teorema dei carabinieri)
Agosto 29th, 2021 | by Marcello Colozzo |
Esercizio
Calcolare

Soluzione
Conviene applicare la proprietà additiva dell'operatore limite:
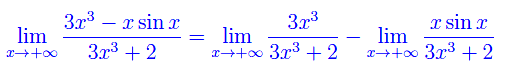
Il primo limite è banale: si calcola per confronto tra infiniti o con il solito artificio:
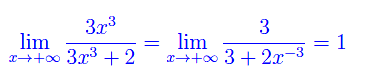
Passiamo al secondo. Osserviamo che

Ma
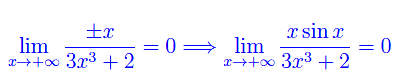
L'ultima implicazione segue dal teorema dei carabinieri. Alternativamente:
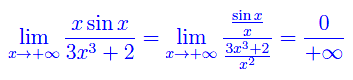
giacché (sinx)/x è infinitesima per |x|->+oo. Ne concludiamo che

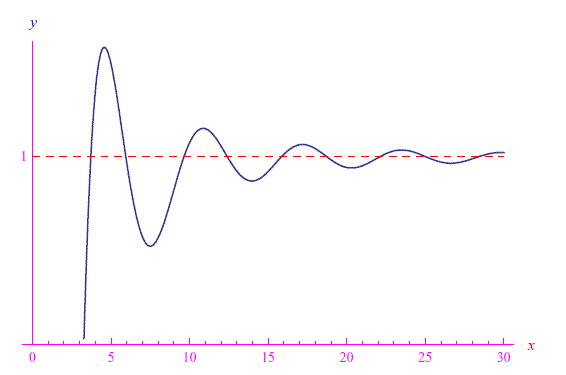
Il grafico della funzione è nella seguente figura. Per x->+oo, la funzione converge a 1, compiendo infinite oscillazioni che si smorzano asintoticamente.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











