» Esercizi svolti di Matematica e Fisica

Matrice metrica di uno spazio unitario

Maggio 14th, 2021 | by Marcello Colozzo |

---

Assegnato unospazio uitario V n-dimensionale, denotiamo con {e_i} una sua base.
Definizione
Chiamiamo matrice metrica asoociata alla predetta base, la matrice quadrata di ordine n, i cui elementi sono

Il prodotto interno di due qualunque vettori di V, si esprime attraverso la matrice metrica. Per mostrare ciò, scriviamo innanzitutto i predetti vettori tramite le loro componenti nella base {e_i}}:

Segue

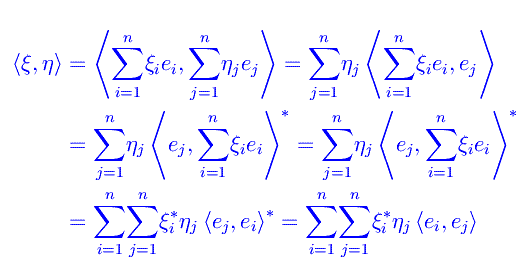
per cui

come volevamo mostrare. Alcune proprietà notevoli della matrice metrica:

Cioè la matrice metrica coincide con la trasposta della matrice complessa coniugata. Come sappiamo dall'algebra lineare, una tale matrice si dice hermitiana.
Inoltre:

Ne segue che comunque prendiamo una n-pla ordinata di numeri complessi (λ₁,λ₂,...,λ_n})

Quindi la matrice metrica è definita positiva.

Tags: matrice metrica, spazio unitario

Articoli correlati