Integrali ellittici di prima, seconda e terza specie
Aprile 19th, 2021 | by Marcello Colozzo |
Seguendo le orme di Smirnov, si dimostra che un qualunque integrale ellittico

è comunque riducibile a integrali del tipo

dove φ(x) è un polinomio e k un intero relativo.
Definiamo rispettivamente integrale ellittico di prima specie, seconda e terza specie gli integrali scritti in fig. 1, quindi dimostriamo
Proposizione
Un qualunque integrale ellittico si esprime come combinazione lineare degli integrali ellittici di prima, seconda e terza specie.
Dim.
Senza perdita di generalità, assumiamo che P(x) sia un polinomio di terzo grado:
Quindi poniamo
Per un intero naturale m non nullo assegnato ad arbitrio, deriviamo
Integrando primo e secondo membro
essendo C una costante di integrazione. Ordinando i vari termini, otteniamo
che è manifestamente una formula di ricorrenza per gli integrali Ik. Per m=0,m=1 otteniamo
cioè un sistema lineare che ci permette di esprimere gli integrali I2,I3 attraverso I0, I1. Per m=2
che esprime I4 attraverso I3,I2,I1. Iterando il procedimento vediamo dunque che per un qualunque k intero positivo, Ik si esprime attraverso I0,I1. Denotando con r il grado del polinomio φ(x), si ha:
da cui la prima parte dell'asserto, giacché Ik si esprime attraverso I0,I1. Per la seconda parte dell'asserto, prendiamo l'integrale
per poi eseguire il cambio di variabile t=x-a, per cui l'integrale diventa
L'asserto segue immediatamente da un procedimento analogo a quello visto nel caso precedente.
Tags: Integrali ellittici di prima specie, integrali ellittici di seconda specie, integrali ellittici di terza specie
Articoli correlati
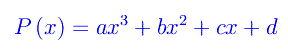

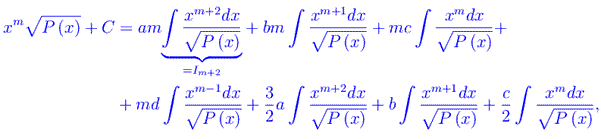
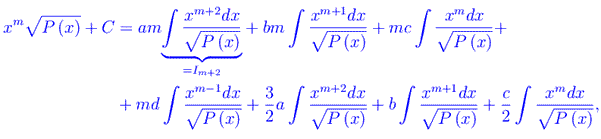



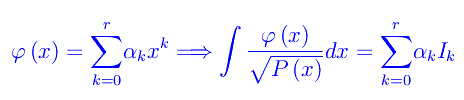
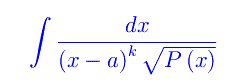
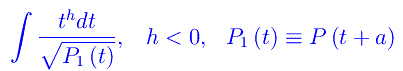


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











