Baricentro di una figura piana
Maggio 30th, 2020 | by Marcello Colozzo |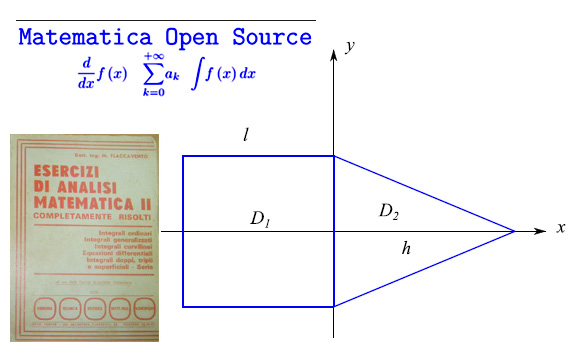
Esercizio n. 11, pag. 241 del Flaccavento.
Si consideri la figura costituita da un quadrato di lato l e da un triangolo isoscele di base l, coincidente con uno dei lati del quadrato, e di altezza h (fig. 1). Calcolare h di modo che il baricentro della figura cada sulla base del triangolo.
Soluzione
Sia G(xG,yG) il baricentro della figura assegnata, la cui simmetria rispetto all'asse y implica yG=0, i.e. il baricentro cade sull'asse x. Ne consegue che G cade sulla base del triangolo se e solo se G coincide con l'origine del riferimento cartesiano, per cui dobbiamo imporre xG=0. Ricordiamo che
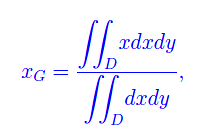
onde
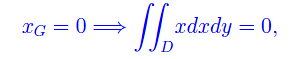
che risolve il problema. Il dominio D si decompone
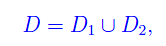
come illustrato in fig. 1.
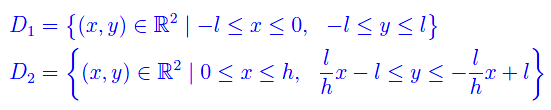
Procedendo per decomposizione per poi applicare le formule di riduzione ai singoli integrali doppi:

Per quanto precede
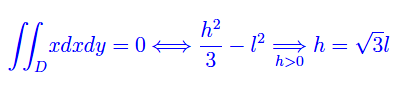
No TweetBacks yet. (Be the first to Tweet this post)
Tags: baricentro, figura piana, integrale doppio
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











