» Esercizi svolti di Matematica e Fisica

[¯|¯] [Serie di funzioni] Teorema del limite

Ottobre 2nd, 2019 | by Marcello Colozzo |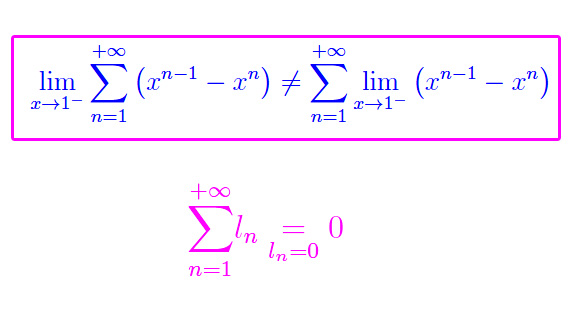

Consideriamo la serie di funzioni

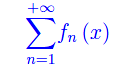
convergente in E (sottoinsieme di R), con somma f(x)

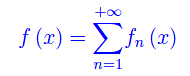
Sia x₀ punto di accumulazione per E, e supponiamo che le funzioni f_n(x) siano ivi convergenti:

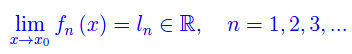
Tale ipotesi implica l'esistenza della serie numerica

per cui ci chiediamo: la predetta serie converge? Una risposta affermativa innesca la questione

ben evidenziata dal punto interrogativo. In altri termini, ci stiamo chiedendo che se in caso di convergenza delle funzioni f_{n}(x), sia possibile scambiare di posto la sommatoria con l'operatore limite:
Continua in pdf.

Tags: convergenza puntiforme, convergenza puntuale, convergenza uniforme, Serie di funzioni, teorema del limite

Articoli correlati