[¯|¯] Disuguaglianza di Schwartz in uno spazio euclideo
Maggio 13th, 2019 | by Marcello Colozzo |
Sia E uno spazio vettoriale propriamente euclideo.
Definizione
Il numero reale non negativo

si dice norma del vettore u.
Da tale definizione segue banalmente

Proposizione (Disuguaglianza di Schwarz)

Dim.
La proposizione è banale se uno dei due vettori è il vettore nullo, per cui consideriamo non nulli entrambi i vettori. Definiamo
Sviluppando il prodotto scalare:
Cioè il trinomio di secondo grado
che è non negativo, in quanto
onde il suo discriminante è non positivo
da cui l'asserto.
Passiamo alla seconda parte del teorema.
in tal caso il trinomio ha un solo zero:
Cioè
c.d.d.
Proposizione (Disuguaglianza triangolare)

Dim.
Riprendendo il trinomio della dimostrazione precedente:
onde l'asserto
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

No TweetBacks yet. (Be the first to Tweet this post)
Tags: disuguaglianza di Schwartz, disuguaglianza triangolare, spazio euclideo
Articoli correlati
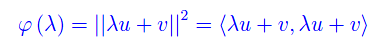
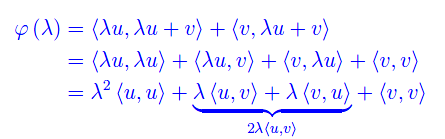
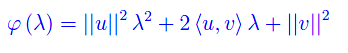

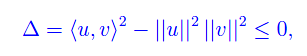
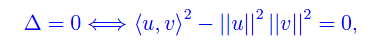






 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









