[¯|¯] Criterio 3 di sommabilità (utile per gli esercizi)
Febbraio 25th, 2019 | by Marcello Colozzo |
Notiamo che la dimostrazione della prima parte del criterio 2 non è invalidata se risulta l=0. Più precisamente, consideriamo il caso

per cui resta dimostrata la sommabilità. Ma l'equazione appena scritta ci sta dicendo che l'infinito f(x) ha ordine indeterminato, ma comunque < 1. Alla stessa maniera, la dimostrazione della seconda parte non è invalidata se risulta l=+oo. Più precisamente, consideriamo il caso

Cioè f(x) è un infinito di ordine indeterminato, ma comunque non inferiore a 1. Resta così dimostrato il criterio:
Criterio 3
Sia f continua in [a,b]-{x0}, con x0 tale che f è ivi infinita:

Sia poi assegnato l'infinito di riferimento

- Se f è un infinito di ordine indeterminato ma comunque < 1, cioè se
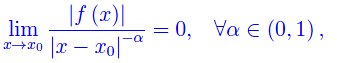
allora f è sommabile in [a,b]. - Se f è un infinito di ordine indeterminato ma comunque non inferiore a 1, cioè se
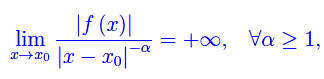
allora f non è sommabile in [a,b].
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: criteri di sommabilità, esercizi, integrale generalizzato
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









