[¯|¯] Come sistemare una palestra rettangolare
Febbraio 3rd, 2019 | by Marcello Colozzo |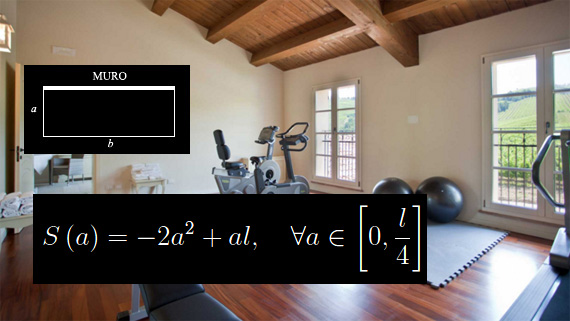
Esercizio
Si chiede di sistemare una palestra rettangolare in modo tale che da tre parti sia chiusa da un reticolato mentre il suo quarto lato sia adiacente a un muro di pietra. Quale è la forma più vantaggiosa (cioè, quella che massimizza la superficie) se si dispone di l metri lineari di reticolato?
Soluzione
Lo schema della palestra è riportato in fig.1. Deve essere

dove l è assegnato una volta per tutte. La superficie è

ovvero tenendo conto della precedente equazione:

Abbiamo, quindi, la funzione:

il cui grafico è un arco di parabola concava per l'origine e il punto di ascissa l/4. Il punto di massimo assoluto di tale funzione è manifestamente l/4, cioè l'ascissa del vertice della parabola. Possiamo comunque verificare, ricercando gli zeri della derivata prima:

onde

Ne consegue

Conclusione: la configurazione geometrica più vantaggiosa è:

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

No TweetBacks yet. (Be the first to Tweet this post)
Tags: funzione, massimo assoluto, massimo relativo, palestra rettangolare
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









