[¯|¯] Velocità vettoriale media e velocità scalare media
Maggio 15th, 2018 | by Marcello Colozzo |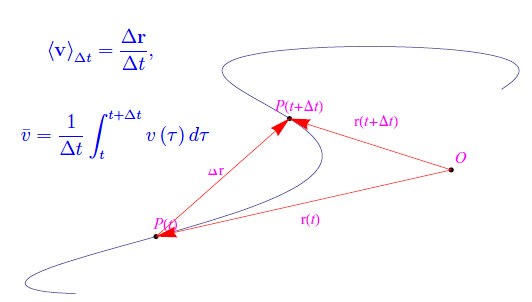
Consideriamo una particella che si muove lungo la seguente traiettoria dello spazio ordinario:
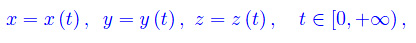
dove t è il tempo, per cui la formula precedente definisce le equazioni orarie del moto che, come è noto, possono essere scritte notazione vettoriale:
essendo
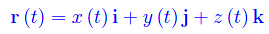
con i,j,k versori degli assi coordinati. Per un assegnato t>0 consideriamo un intervallo di tempo Δt tale che
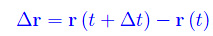
che definisce l'incremento (o il decremento) del vettore posizione della particella nel predetto intervallo di tempo. Come è noto, la
velocità vettoriale media nell'intervallo Δt è la grandezza:
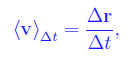
Dalla fig. 1 vediamo che abbiamo denotato con P(t) e P(t+Δt) le posizioni della particella ai tempi t e t+Δt rispettivamente, per cui è univocamente determinato l'arco di traiettoria avente per estremi i predetti punti. Ciò ci consente di definire la velocità scalare media:
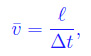
essendo l la lunghezza dell'arco di estremi P(t) e P(t+Δt). Dalla geometria differenziale
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
