[¯|¯] Introduzione all'insieme di Cantor
Aprile 6th, 2017 | by Marcello Colozzo |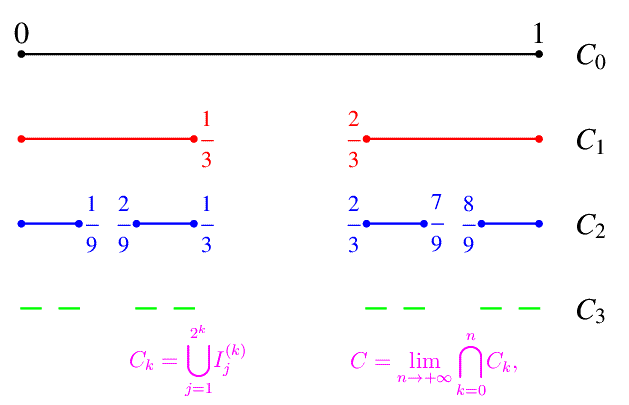
Fig. 1
L'insieme di Cantor è un oggetto tutt'altro che maneggevole, per cui procederemo per gradi. In questo post vedremo come "costruire manualmente" il suddetto insieme. Concettualmente è molto semplice: si tratta di un procedimento ricorsivo che parte dall'intervallo chiuso [0,1] e lo divide in tre "parti" uguali (quindi, ciascuna di ampiezza 1/3), dopodichè si rimuove l'intervallo centrale. Il procedimento viene ripetuto sugli intervallini estremi, e così via all'infinito. La difficoltà iniziale coniste nel "matematizzare" il procedimento. Ed è proprio questo lo scopo dell'articolo odierno.
Assegnato un intervallo chiuso [a,b] di R, qundi di ampiezza Δ=b-a eseguiamo una
decomposizione D([a,b]) di norma δ=Δ/3 attraverso l'insieme di punti equispaziati:
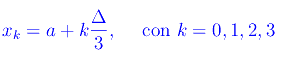
Cioè
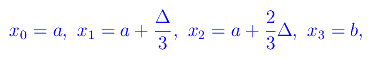
come appare in figura:

Consideriamo l'intervallo centrale:
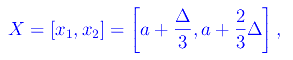
il cui interno è l'aperto
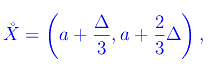
e il complementare in [a,b] è:
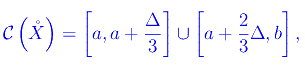
rappresentato di seguito:

In altri termini, questo insieme è ottenuto rimuovendo da [a,b] l'intervallo centrale (x1,x2). Formalmente ciò può essere visto come il risultato dell'azione di una applicazione
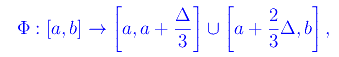
schematizzata in figura:
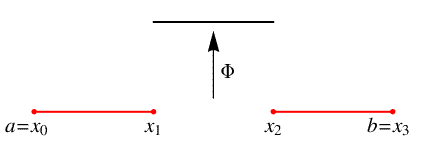
Il procedimento appena visto può essere ripetuto sugli intervalli parziali
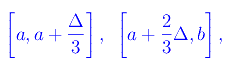
facendo cioè agire l'applicazione sui predetti intervalli. Ci proponiamo di determinare il risultato di un numero infinito di iterazioni del procedimento. A tale scopo focalizziamo la nostra attenzione sull'intervallo chiuso [0,1], anziché su un generico intervallo [a,b].
Più specificatamente, per un assegnato intero naturale k costruiamo per ricorrenza 2k intervalli contenuti in [0,1] e a due a due disgiunti:
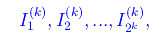
La ricorrenza è definita da
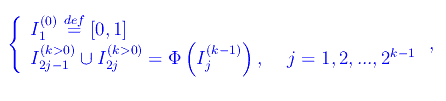
che per k=1 restituisce
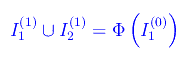
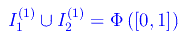
Per quanto precede
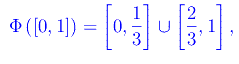
onde
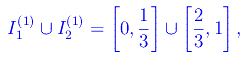
vale a dire
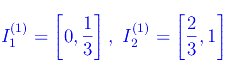
Per k=2 è j=1,2, per cui la formula per ricorrenza restituisce
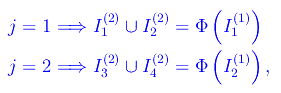
da cui vediamo che per determinare gli intervalli
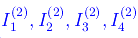
dobbiamo esplicitare l'azione dell'applicazione su
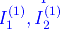
calcolati in precedenza. Abbiamo
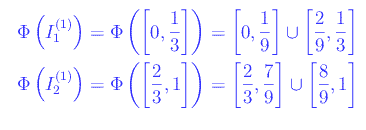
Tale procedimento è illustrato nelle figure seguenti:
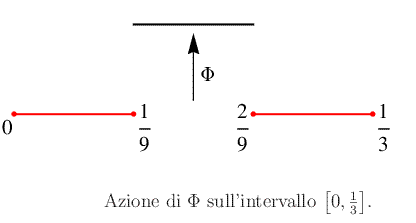
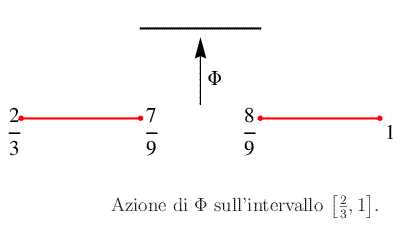
Segue
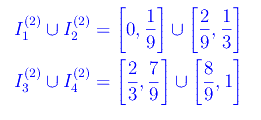
Cioè
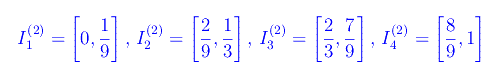
Tale procedimento ricorsivo, per ogni k restituisce univocamente 2k intervalli contenuti in [0,1] e a due a due disgiunti, la cui unione è
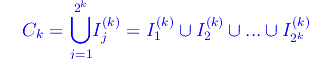
Precisamente
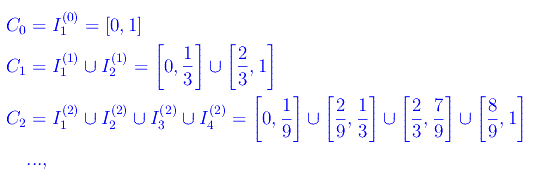
come riportato in fig. 1.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: insieme di cantor, insieme perfetto, insieme ricorsivo, misurabilità dell'insieme di cantor
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











