» Esercizi svolti di Matematica e Fisica

[¯|¯] Premesse topologiche

Aprile 1st, 2017 | by Marcello Colozzo |

---

A un qualunque insieme S possiamo univocamente associare l'insieme i cui elementi sono tutti e soli i sottoinsiemi di S. Denotando con P(S) tale insieme, si ha:

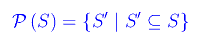
Definizione
Chiamiamo P(S) insieme delle parti di S.
L'insieme della parti di S è "strutturalmente" più complicato di S. Ad esempio, consideriamo l'insieme il cui unico elemento è la lettera a:

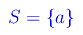
I sottoinsiemi di S sono:

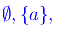
onde

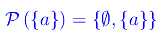
Aggiungiamo un elemento:

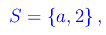
i cui sottoinsiemi sono

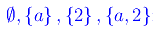
Quindi

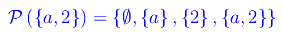
Se S è il vuoto? Cioè

Segue

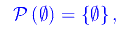
ovvero l'insieme delle parti del vuoto è l'insieme il cui unico elemento è il vuoto. Viceversa

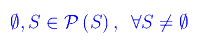
Proposizione

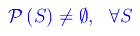
Dimostrazione

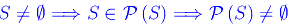
c.d.d.









Definizione
Sia Θ un sottoinsieme non vuoto di P(S) (cioè Θ è un insieme i cui elementi sono sottoinsiemi di un assegnato insieme S). Diciamo che Θ è una topologia per S, se sono verificate le seguenti proprietà:

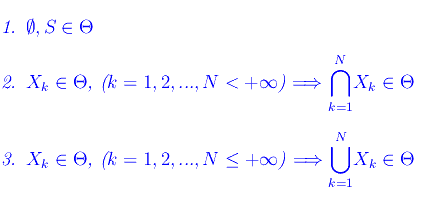
La coppia ordinata (S,Θ) si chiama spazio topologico. Gli elementi di Θ sono gli insiemi aperti o semplicemente gli aperti di S. Gli elementi di S sono i punti dello spazio topologico (S,Θ). Gli insiemi chiusi di S sono, invece, tutti e soli i sottoinsiemi di S il cui complementare (in S) è aperto.

Proposizione

Dimostrazione
Il primo assioma è banalmente verificato. Riesce:

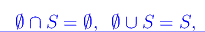
per cui sono verificati gli assiomi 2 e 3.
c.d.d.
Definizione
La topologia

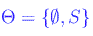
è detta topologia banale.
Proponiamo un esempio suggestivo sulla topologia banale. Sia S_π l'insieme dei pensieri elaborati da una mente M:

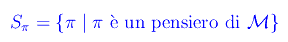
Chiamiamo tale insieme (non vuoto!) spazio della mente M. La topologia banale per S_π è:

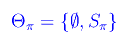
I pensieri elaborati da M sono, dunque, i "punti" dello spazio topologico (S_π,Θ_π), mentre gli aperti di S_π sono Ø e S_π. Evidentemente:

Ne concludiamo che l'insieme dei nostri pensieri può essere strutturato come spazio topologico.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

---

---

Tags: aperti, spazio topologico, topologia, topologia banale

Articoli correlati