[¯|¯] Proprietà e teoremi su infinitesimi e infiniti

Marzo 1st, 2017 | by Marcello Colozzo |

infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Fig. 1. Le funzioni f1(x)=2(1-cosx) e f2(x)=x² sono infinitesimi equivalenti per x->0. Pertanto hanno la stessa parte principale rispetto all'infinitesimo g(x)=sinx. Geometricamente significa che i rispettivi grafici tendono a sovrapporsi in un intorno di x=0.

Proposizione
Siano f1(x) e f2(x) due infinitesimi equivalenti (per x->x0).
Se fk(x) (k=1,2) è dotato di parte principale rispetto a g(x), si ha che fh(x) (con h diverso da k) è dotato di parte principale (rispetto a g(x)) e le due parti principali coincidono.
Dimostrazione
Sia

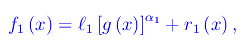
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

cosicché
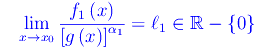
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Per ipotesi f1(x) e f2(x) sono equivalenti:

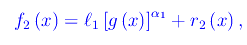
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Segue
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Pertanto
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

onde l'asserto.
c.d.d.
Esempio
Consideriamo gli infinitesimi in x=0:
infinitesimi,proprietà, parte principale,infinitesimi di riferimento









Tenendo conto del limite fondamentale
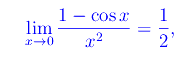
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

segue immediatamente
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

onde l'equivalenza degli infinitesimi assegnati. Determiniamo la parte principale di f1(x) rispetto all'infinitesimo g(x)=sinx. Innanzitutto calcoliamone l'ordine:

infinitesimi,proprietà, parte principale,infinitesimi di riferimento

cosicché f1(x) è del second'ordine rispetto a g(x), ed ammette la seguente decomposizione:
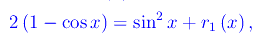
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

per cui
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Per la proposizione precedente:s

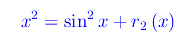
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

Cioè

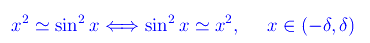
infinitesimi,proprietà, parte principale,infinitesimi di riferimento

I vari andamenti sono illustrati in fig. 1.








No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio