[¯|¯] Parte principale di (π/2 - arctanx)-1/2 (per x->+oo)

Marzo 1st, 2017 | by Marcello Colozzo |

infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Fig. 1. La parte principale dell'infinito f(x)=1/x² è la funzione medesima.

Consideriamo la funzione

infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Riesce
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

onde f(x) è un infinito per x->+oo. Ricerchiamone l'ordine assumendo come infinito di riferimento la funzione v(x)=x. Abbiamo
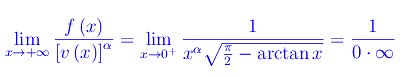
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Eseguiamo il cambio di variabile:

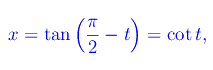
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

da cui
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

onde
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Ciò implica che f(x) è un infinito di ordine 1/2. Inoltre

infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Quindi la parte principale è
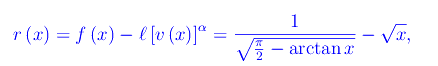
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Segue
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

che è un infinito di ordine minore di 1/2. Infatti:

infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore









La formula di decomposizione si scrive:

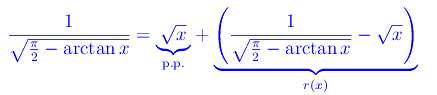
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

Quindi

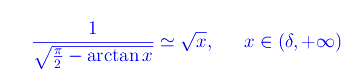
infiniti, parte principale di un infinito, formula di decomposizione di un infinito,termine di ordine inferiore

In altri termini, per x»1 la funzione va come vx. Ciò è illustrato in fig. 1.








No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio