» Esercizi svolti di Matematica e Fisica

[¯|¯] Integrale curvilineo di una funzione

Novembre 15th, 2016 | by Marcello Colozzo |

Sia f una funzione reale delle variabili reali x,y,z, definita in un dominio di R³ ed ivi continua. Assegnata una curva regolare contenuta in D, di rappresentazione parametrica naturale

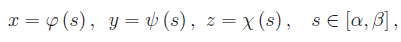
eseguiamo una decomposizione D dell'intervallo [a,b], prendendo ad arbitrio n+1 punti s0,s1,...,sn tali che:

Denotiamo con P_k il punto di γ di ascissa curvilinea s_k. Quindi

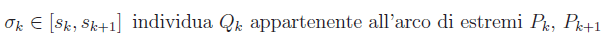
Costruiamo la somma










Se Δ è la norma della decomposizione, cioè

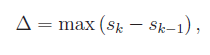
poniamo

che è l'integrale curvilineo di f(x,y,z) esteso alla curva γ di estremi P,Q.

Scarica gli appunti in pdf

Tags: curva regolare, integrale curvilineo, rappresentazione naturale, somma integrale

Articoli correlati