» Esercizi svolti di Matematica e Fisica

[Fisica 1] Variante dell'esercizio precedente

Esercizio tratto da [1]. La soluzione è nostra

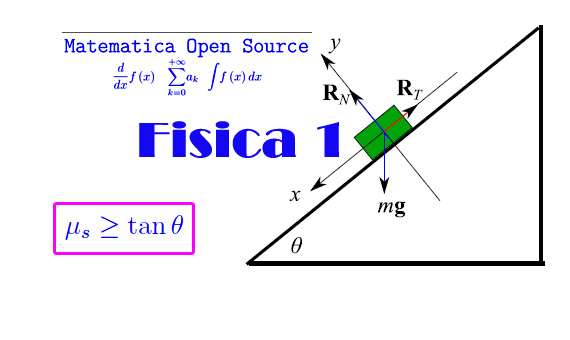
Nel sistema considerato nel problema precedente, si supponga che il piano inclinato risulti scabro con coefficiente di attrito dinamico µ_d=0.1, e che inizialmente i due corpi si muovano con velocità v₁=3m/s positiva nel sistema di riferimento considerato precedentemente. Si determini la posizione e l'istante in cui il punto A inverte il moto, assumendo la posizione iniziale dei due corpi come origine degli assi coordinati dei rispettivi sistemi di riferimento. Si determini anche la legge del moto e la tensione della fune.

Scarica la soluzione in pfd.

Posted in Fisica generale 1 | No Comments »

Equilibrio su piano inclinato scabro

Stabilire le condizioni di equilibrio per un blocco di massa m appoggiato su un piano inclinato di θ, che presenta un coefficiente di attrito statico µ_s.

Soluzione
Riferiamoci alla fig. 1, dove abbiamo istituito un sistema di assi cartesiani ortogonali x,y.

Denominanto con R_N e R_T rispettivamente la reazione normale e la reazione tangenziale (attrito) del vincolo, la condizione di equilibrio si scrive:

Posted in Fisica generale 1 | No Comments »