Coronavirus. Famiglia di logistiche
Marzo 16th, 2020 | by Marcello Colozzo |
Abbiamo visto che il parametro α è una funzione del tempo (variabile deterministica o aleatoria che sia). Ne consegue che il giusto approccio al problema non è quello di tirar fuori una qualche logistica che sia in grado di simulare la diffusione virale. Ricordiamo infatti, che la logistica caratterizza un sistema dinamico autonomo, nel senso che l'equazione differenziale non contiene esplicitamente la variabile t. Qui, invece, si ha un'equazione del tipo
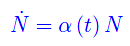
che integrata con la condizione iniziale N(0)=N0, fornisce la soluzione a tutti i tempi:
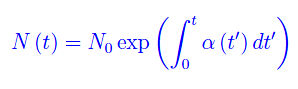
È chiaro che l'elemento veramente ignoto è proprio la funzione α(t), che è ottenibile per interpolazione sui dati disponibili, ma solo nell'intervallo di tempo T(t1)=[0,t1] essendo t1 l'istante attuale. Per t > t1 siamo fuori range, per cui tale modello nulla potrà dirci sul comportamento futuro dell'espansione virale. Possiamo comunque utilizzare un modello basato sulla logistica, nel modo che segue. Assegnato t1, scriviamo:
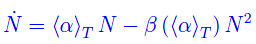
In questa equazione differenziale, il valor medio <α>T svolge il ruolo di parametro, per cui non abbiamo una sola logistica ma una famiglia di logistiche ad un parametro

come mostrato in fig. 1.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico












By Angheran on Mar 16, 2020
Il tasso di letalità cresce linearmente dal 2 Marzo , come 0,37 al giorno. Puoi aggiornare anche twitter?
By Marcello Colozzo on Mar 16, 2020
secondo me è preferibile concentrarsi sul tasso di contagiati, perchè il tasso di mortalità è più lento in quanto le terapie diventano progressivamente più efficaci con il passare dei giorni.
Il tasso di contagiati è sicuramente sotto stimato, inoltre è un "dato sporco", ma è l'unico disponibile.
ps. sto aggiornando twitter
By Angheran on Mar 16, 2020
Potrebbe tornare utile il modello Thomas-Fermi con la famosa trasformazione di Majorana in eq di Riccati ?(in realtà di Abel)
By Marcello Colozzo on Mar 16, 2020
non penso, perché l'equazione di Riccati si integra con un cambio di variabile. Semmai il problema è un altro, cioè in questo modo si cerca di approssimare un sistema non autonomo in uno autonomo. Infatti, l'equazione di Riccati impostata in quel modo, non contiene esplicitamente il tempo.