[¯|¯] Differenziabilità di una funzione vettoriale di variabile vettoriale (parte 2)
Febbraio 10th, 2020 | by Marcello Colozzo |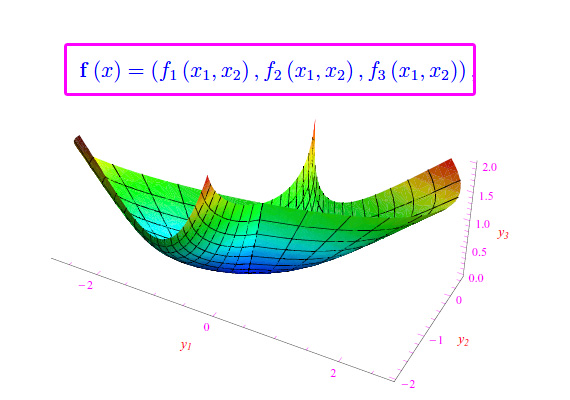
A questo punto ci chiediamo: "cos'è Λ(u)?" Per quanto precede, tale funzione vettoriale lineare (della variabile u) è la derivata della funzione vettoriale f(x) secondo la direzione u, calcolata in x0:

Si noti che Λ(u) dipende anche da x0, che tuttavia si comporta alla stregua di un parametro, giacché noi fissiamo tale punto per poi calcolare la derivata secondo la predetta direzione. Se ques'ultima è definita da uno dei vettori di base, per quanto già stabilito:

Ora riscriviamo l'incremento di f

Riesce

Ne consegue

dove il penultimo passaggio segue dalla linearità di Λ. Tenendo presente che hu è l'incremento della variabile (vettoriale) indipendente:

Quindi

cioè Λ(hu) è il differenziale di f calcolato in x0. Quindi la differenziabilità della funzione vettoriale si riesprime:

dove

A questo link un esercizio svolto.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











