[¯|¯] Funzioni vettoriali lineari

Febbraio 5th, 2020 | by Marcello Colozzo |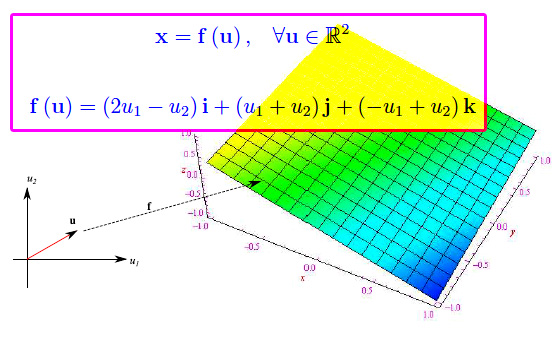

In questa lezione definiamo le funzioni vettoriali lineari. Il lettore che mastica un pò di algebra lineare capirà al volo che stiamo parlando degli omomorfismi tra spazi vettoriali (finito-dimensionali). Ne consegue che una funzione vettoriale è univocamente determinata dalla sua matrice rappresentativa rispetto a basi assegnate dei predetti spazi vettoriali, ed è chiaro che gli elementi di matrice cambiano se si esegue un cambiamento di base.

Nel file pdf seguirà un esempio istruttivo che mostra una chiara interpretazione geometrica di una funzione lineare in cui la variabile vettoriale indipendente appartiene allo spazio vettoriale euclideo 2-dimensionale, mentre la variabile dipendente è un elemento dello spazio vettoriale euclideo 3-dimensionale. In questo caso speciale, una funzione lineare non fa altro che trasformare tutto R^2 in un piano di R^3.

Scaria la lezione in pdf

No TweetBacks yet. (Be the first to Tweet this post)