» Esercizi svolti di Matematica e Fisica

[¯|¯] Per Alice il proiettile colpisce il bersaglio PRIMA e DOPO viene sparato

Gennaio 8th, 2019 | by Marcello Colozzo |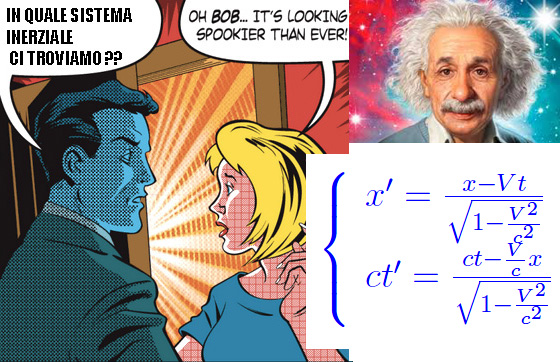

Le trasformazioni galileiane sono un caso particolare delle trasformazioni di Lorentz [1]:

nel senso che per V«c si riducono (eseguendo uno sviluppo di Taylor) alle trasformazioni galileiane. Le TL sono facilmente invertibili operando la sostituzione V -> (-V), x -> x', t -> t':

È ovvio che dovrà essere V < c, affinchè le varie grandezze siano reali. Operando come nella sezione precedente, troviamo l'equazione dell'asse ct':

che coincide con quella galileiana. Mentre l'asse x' è

ovvero una retta per l'origine e di coefficiente angolare V/c. Gli assi x' e ct' sono simmetrici rispetto alla bisettrice del primo e terzo quadrante

come illustrato in fig.

Immaginando di aumentare la velocità dell'auto di Alice, vediamo che gli assi x',ct' ruotano attorno all'origine del riferimento x-ct, il primo in senso antiorario e il secondo in senso orario. In particolare se

per i cui i predetti assi si sovrappongono alla posizione limite rappresentata dalla bisettrice ct=x. Si osservi che quest'ultima è la linea di universo di una particella che si muove a velocità c. La disuguaglianza V > c implica un moto superluminale per l'auto di Alice. Geometricamente, vediamo che il riferimento x'-ct' che definisce lo spaziotempo relativo al sistema inerziale in cui Alice è in quiete, perde di significato in quanto gli assi si invertono.

La novità introdotta dalle trasformazioni di Lorentz consiste nel fatto che a differenza del caso precedente, Alice e Bob non sono d'accordo sull'istante in cui il proiettile colpisce il bersaglio. Infatti, dalla seconda delle TL:

ove x(t) è l'equazione oraria del moto del proiettile rispetto a Bob. Cioè

Quindi

avendo definito la grandezza adimensionale

che ci dice come cambia la scala dei tempi passando da un sistema inerziale all'altro. Nel limite galileiano

da cui l'invarianza della coordinata tempo sotto trasformazioni galileiane. Diversamente:

ovvero Alice e Bob non sono d'accordo sul tempo segnato dai rispettivi orologi. In particolare, abbiamo che t₀=0 è

l'istante di sparo per entrambi, giacché dall'eqazione scritta più sopra segue

Mentre riguardo all'istante in cui il proiettile colpisce il bersaglio, si ha

Se poi

riesce

ossia Alice vede il proiettile colpire il bersaglio prima di essere sparato. Inoltre

Conclusione
Condizione necessaria affinché Alice vede il proiettile colpire il bersaglio prima di essere sparato è che la velocità del proiettile sia maggiore della velocità della luce. La condizione diviene sufficiente se la velocità del proiettile è maggiore di c²/V, esssendo V la velocità di Alice.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: proiettile, Sistema di riferimento inerziale, trasformazioni galileiane

Articoli correlati