[¯|¯] Momento di una forza rispetto a un punto

Novembre 16th, 2018 | by Marcello Colozzo |

In alcune lezioni precedenti, abbiamo visto che secondo principio della dinamica

può esprimersi attraverso la quantità di moto p=mv

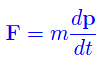
Tuttavia nei casi in cui la traiettoria è curvilinea, riesce più utile una nuova formulazione basata su nuove grandezze. Supponiamo, ad esempio, di avere una forza F applicata in un punto P, come illustrato in fig. 1. Assegnati ad arbitrio un punto O di τ, dove τ è la retta di azione di F, denotiamo con r il vettore posizione di P rispetto ad O.

Definizione
Dicesi momento della forza F rispetto ad O, il vettore

Se θ è l'angolo tra i vettori F ed r, si ha:

Il vettore M è perpendicolare al piano individuato dai vettori r ed F, ed è orientato in modo che la terna (r,F,M) risulti levogira. Se abbassiamo da O la perpendicolare a τ, l'equazione precedente diviene

essendo

ovvero la distanza tra O e la retta τ.

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Definizione
Il numero reale non negativo b si dice braccio della forza F.

Dalla relazione M=Fb segue che comunque spostiamo i punti P ed O su τ e τ' rispettivamente, il momento di F non cambia. Dalla M=rFsin(θ) vediamo poi che se r ed F sono vettori non nulli, il momento è nullo se e solo se b=0, i.e. O appartiene a τ. Infine, se O è l'origine di una terna di assi cartesiani ortogonali xyz, si ha che M è lo sviluppo del determinante simbolico riportato in fig. 1, dove: i,j,k sono i versori degli assi coordinati; x,y,z le componenti cartesiane del vettore r, i.e. le coordinate cartesiane di P; F_x,F_y,F_z le componenti cartesiane del vettore F. Segue

La definizione di momento si generalizza a un sistema di forze. Precisamente se al punto P della fig. 1 sono applicate le forze F₁,F₂,...,F_N, denotando con F la risultante:

si ha che il momento di F rispetto ad O è:

è il vettore della k-esima forza, onde:

Ne concludiamo che il momento della forza risultante è il risultante dei momenti delle singole forze applicate.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Vai alla lezione successiva

Vai alla lezione precedente

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)