» Esercizi svolti di Matematica e Fisica

[¯|¯] Diagonalizzazione di una matrice in ambiente Mathematica

Assegnata una matrice quadrata di ordine n su un campo K:

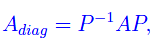
dove P è un'opportuna matrice, mentre A_diag è diagonale. Per un noto teorema, A diagonalizzabile se e solo se ammette n autovettori linearmente indipendenti. In tal caso il sistema di autovettori è una base dello spazio vettoriale Kn, e la matrice P è la matrice di passaggio dalla base canonica del predetto spazio alla base degli autovettori. Ne consegue che la diagonalizzazione di una matrice si riduce al problema della ricerca degli autovalori e dei corrispondenti autovettori. Problema a volte rognoso, data la mole di calcoli.

Vediamo come risolverlo rapidamente con Mathematica, considerando il seguente esempio:

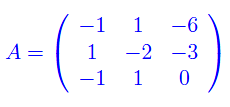
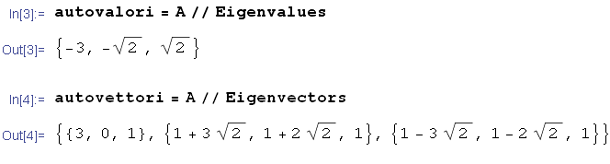
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: autovalori, autovettori, diagonalizzazione di una matrice, Mathematica