[¯|¯] Esercizio svolto sui tensori controvarianti di rango 2
Giugno 6th, 2017 | by Marcello Colozzo |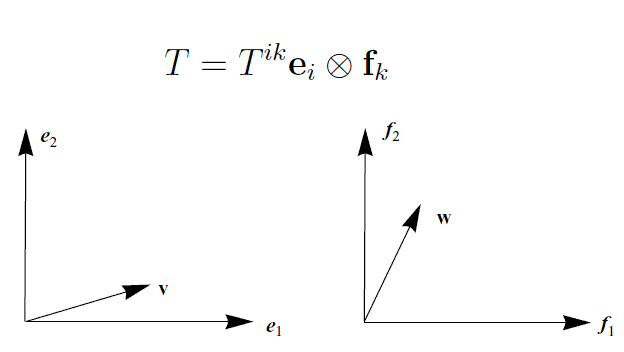
Consideriamo il prodotto tensoriale di due spazi 2-dimensionali E2 e F2 sul campo reale R. Se {e1,e2} e {f1,f2} sono due basi dei predetti spazi vettoriali, si ha:

Osservazione
Per quanto detto in in precedenza avremmo dovuto scrivere:
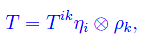
ove ηi e ρk denotano le forme lineari che compongono le rispettive basi biduali. D'altra parte, queste ultime si identificano a meno di un inessenziale isomorfismo naturale, con le rispettive basi degli spazi vettoriali assegnati. In tal modo è giustificata la formula precedente.
Senza perdita di generalità, supponiamo che E2 e F2 siano strutturati come spazi euclidei e che le predette basi siano ortonormali (cfr. fig. 1):
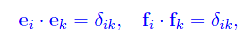
dove · denota il prodotto scalare.
Segue
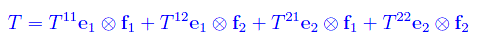
Osserviamo infine che il prodotto tensoriale degli spazi vettoriali E2 e F2 è isomorfo al prodotto cartesiano E2×F2, giacché si tratta di spazi vettoriali isodimensionali (per un noto teorema l'isodimensionalità è condizione necessaria e sufficiente per l'isomorfismo):
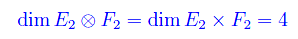
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











