» Esercizi svolti di Matematica e Fisica

Interpretazione cinematica dei punti cuspidali

In molti testi di Analisi Matematica 1 è riportata un'interessante interpretazione dei punti cuspidali. Più specificatamente, se P₀(x₀,f(x₀)) è un punto cuspidale per la curva y=f(x), il vettore velocità di un punto mobile lungo la medesima curva subisce nel punto cuspidale un'inversione istantanea d'orientamento, conservando la direzione. Per tale ragione, tali punti sono noti come punti di regresso.

La suddetta interpretazione cinematica è in realtà errata, in quanto è necessario aggiungere che la componente della velocità nella direzione dell'asse y diverge (positivamente o negativamente) a sinistra di x0, e diverge (negativamente o positivamente) a destra di tale punto. In altri termini, quando il punto transita per la cuspide, si assiste a un'inversione istantanea del vettore velocità, ma il modulo di quest'ultimo diviene infinitamente grande. È chiaro, allora, che un tale moto è relativisticamente impossibile in quanto contraddice uno dei postulati della Relatività Speciale secondo cui l'esremo superiore dell'insieme dei valori assunti dalle velocità di particelle massive è pari alla velocità della luce nel vuoto. Non sono, cioè, possibili moti superluminali e, a più forte ragione, a velocità infinita.

Per elaborare un esempio numerico, abbiamo considerato una traiettoria "patologica" cioè dotata di almeno un punto di regresso (cfr. fig. al top). Si tratta di una curva integrale del sistema di equazioni differenziali:

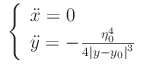
che regolano il moto piano di una particella di massa m che si muove in un campo di energia potenziale (buca infinitamente profonda):

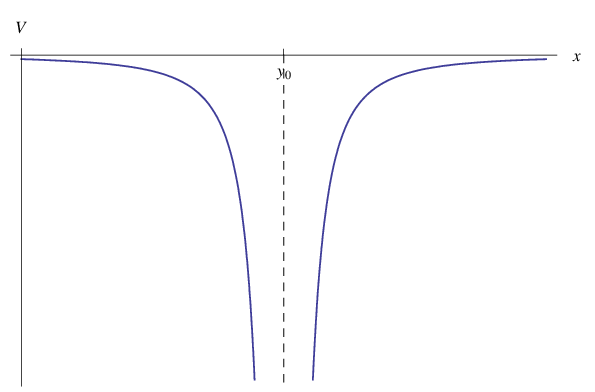
Man mano che la particella si avvicina alla singolarità, il potenziale del campo di forze diviene progressivamente più intenso e tale sarà il modulo della forza che ne deriva. Quest'ultima incurverà la traiettoria fino al transito per il punto di regresso, dove risulterà tangente alla retta verticale per x0.

Per i dettagli matematici, scarica il file pdf seguente:
punti_regresso.pdf

Tags: Cinematica, punti cuspidali, punti di regresso, relatività speciale