[¯|¯] Variabili aleatorie nell'ambiente di calcolo Mathematica
martedì, Marzo 14th, 2017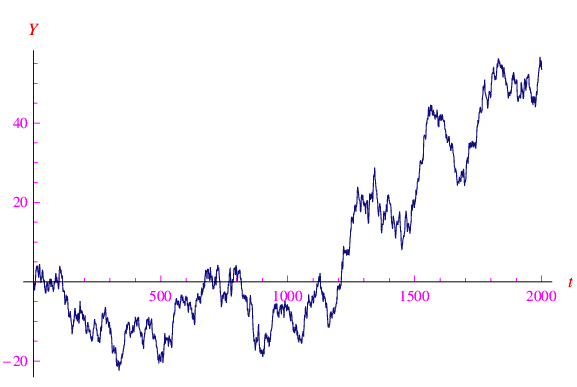
Fig. 2
Variabili deterministiche e variabili aleatorie
Abbiamo appreso in maniera euristica la differenza tra variabili deterministiche e variabili aleatorie. Cerchiamo ora di assiomatizzare tali nozioni.
Le variabili deterministiche -- che denotiamo con ydet(t), dove t è il tempo -- sono soluzioni di un assegnato problema di Cauchy, per cui non sono altro che ordinarie funzioni dell'Analisi matematica. Quindi:

che si legge: il valore che ydet(t) assume all'istante t'>t è univocamente determinato dal valore all'istante t. Nel caso aleatorio:
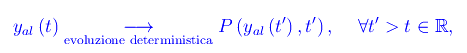
dove P(yal(t'),t') è la probabilità che al tempo t'>t la variabile aleatoria assuma il valore yal(t'), per cui il valore di yal al tempo t non determina univocamente il valore di yal nel generico istante successivo t, ma determina il valore della probabilità. In altri termini, per definire una variabile aleatoria è necessario conoscere la probabilità
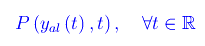
Si tratta di una grandezza che dipende dal tempo t sia esplicitamente che implicitamente (cioè attraverso yal). Ciò implica
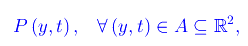
dove abbiamo omesso il pedice "al" e assunto y variabile con continuità in [y1,y2], per cui
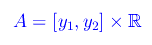
Senza perdita di generalità supponiamo
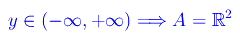
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











