Simulazione del processo di carica di un condensatore attraverso una Macchina Ricorsiva Lineare

sabato, Marzo 26th, 2016

Estratto del Capitolo 4 del libro "Macchine ricorsive" di prossima pubblicazione:
(altro…)

Posted in News | 1 Comment »

Un esempio di applicazione della salita esponenziale: il transitorio circuitale di una serie RC

lunedì, Febbraio 8th, 2016

funzione unit step, salita esponenziale, transitorio circuitale, serie RC

Premessa: per i dettagli matematici, leggi il file pdf

Nel post precedente abbiamo esaminato il comportamento asintotico della salita esponenziale. Tale funzione ha un'istruttiva applicazione nei transitori circuitali. Consideriamo in paricolare la seguente serie RC:

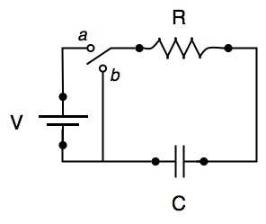
la resistenza R e il condensatore di capacità C, sono collegati in serie e alimentati da una d.d.p. costante pari a V. Se a t=0 chiudiamo il circuto, la carica elettrica sulle armature di C segue una salita esponenziale. Precisamente:

dove

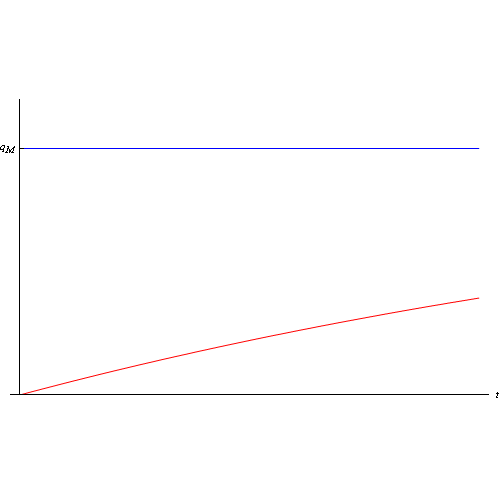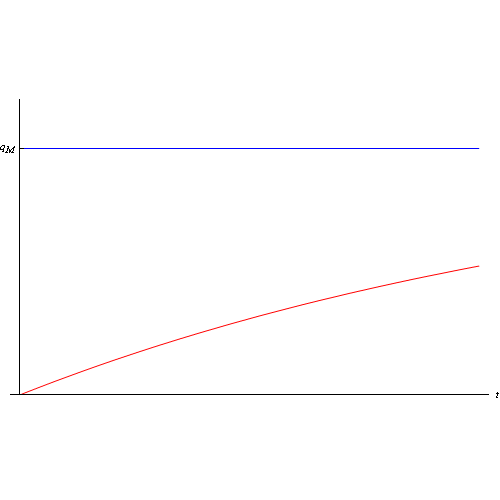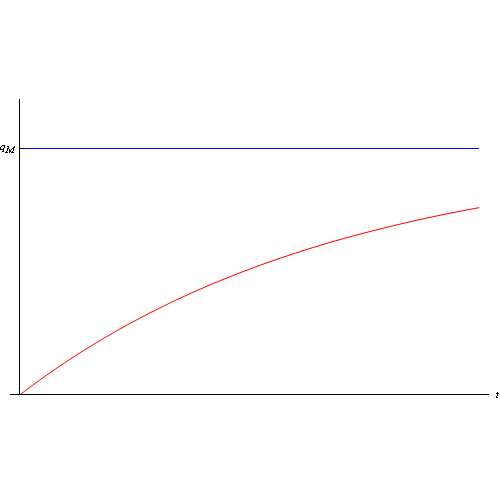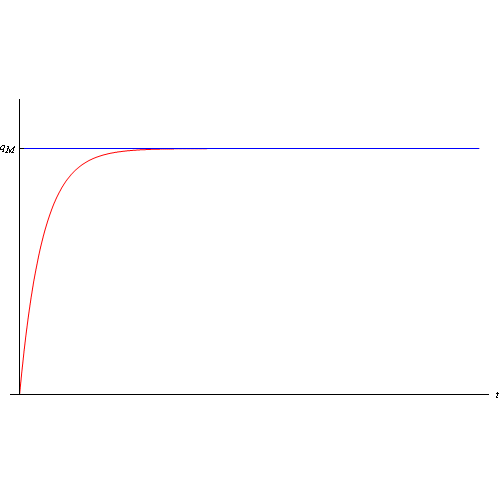
è la costante di tempo della serie RC, ed ha le dimensioni di un tempo. È facile convincersi che tale grandezza fissa la scala dei tempi di carica del condensatore. Maggiore è tale costante, più lungo sarà il processo di carica, e viceversa. L'altra costante, invece, è:

che ha le dimensioni di una carica elettrica.

Il grafico della q(t) è:

Supponendo di poter realizzare una condizione ideale in cui la resistenza R è nulla (si pensi ad un condensatore ideale, privo cioè di resistenza ohmica), si ha che la costante di tempo si annulla e, conseguentemente, il processo di carica è istantaneo o, ciò che è lo stesso la funzione q(t) segue un gradino unitario (unit step). Per valori non nulli della costante di tempo, scriviamo allora la funzione q(t) come: