[¯|¯] Il libero arbitrio: una questione termodinamica?

sabato, Novembre 29th, 2014

Dalla condivisione dello stato di Facebook di uno dei miei contatti:

mi sono venute alcune idee sulla questione del cosiddetto libero arbitrio. Una precisazione: le suddette idee vanno prese con le molle, perchè si tratta di speculazioni (deliri? 🙂 ) e nulla di più.
Ciò premesso, denotiamo con X un qualunque sistema cognitivo (umano, calcolatore). In poche parole, X è un sistema "in grado di pensare" e, soprattutto di ricordare (in effetti, il nocciolo della questione è legato alla memoria). Osserviamo subito che se X è un calcolatore, la sua memoria è praticamente infallibile. Ciò è dovuto al valore estremamente basso dell'entropia dei suoi stati logici. Infatti, la memoria di un calcolatore è un sistema a due stati, e utilizzando la nota formula (dalla meccanica statistica), si ottiene per l'entropia (k_B è la costante di Boltzmann):

entropia,termodinamica,meccanica statistica

Se, invece, X non è un calcolatore:

dove 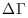è il volume dello spazio delle fasi associato al sistema, i.e. il numero di stati di singola particella. È chiaro che qui 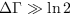, onde una qualunque interfaccia umana avrà un'entropia del proprio sistema cognitivo, maggiore dell'entropia della memoria di un calcolatore. In altre parole, un calcolatore ha una "memoria infallibile" proprio perchè è un sistema "più ordinato".
(altro…)