Periodicità di una tassellatura del piano. La congettura di Wang

domenica, Agosto 15th, 2021

tassellatura del piano, periodicità, congettura di wang — **Fig. 1**

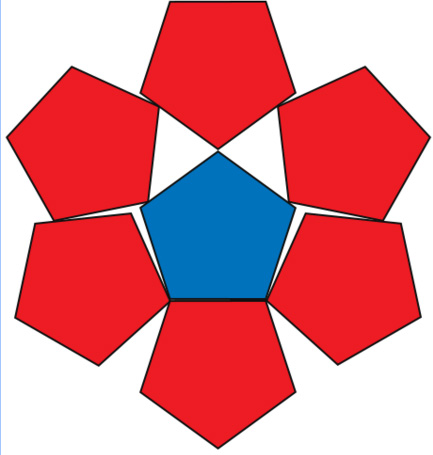
Per parlare ancora di tassellatura del piano, introduciamo alcune analogie con la fisica, osservando preliminarmente che la tassellatura di fig. 1 proposta dall'artista Erasmo Falanga è "globalmente asimmetrica", ma potrebbe non esserlo localmente. Per essere più precisi, a noi interessa una simmetria per traslazione, nel senso che un ente geometrico è invariante per traslazione se e solo se rimane immutato comunque lo "spostiamo" nello spazio ambiente (nel caso in esame lo spazio ambiente è il piano euclideo). Peraltro, la nozione di simmetria è fondamentale in fisica teorica, giacché una simmetria è sempre associata a una grandezza che si conserva. Ad esempio, se l'energia di un sistema fisico è invariante per traslazione spaziale, il sistema conserva la quantità di moto (prodotto della massa inerziale del corpo per la sua velocità). Se, invece, l'energia è invariante per evoluzione temporale (una locuzione equivalente è "traslazione temporale"), il sistema conserva l'energia.
Quanto appena esposto è una proprietà generale nota come Teorema di Noether.
(altro…)

Posted in Arte e Scienza | No Comments »

Tassellatura del piano. Rudimenti topologici

martedì, Luglio 27th, 2021

tassellatura del piano,penrose,topologia

Ricordiamo brevemente che nello spazio euclideo Rn un dominio è la chiusura di un aperto. Riferiamoci in particolare al piano euclideo R², denotando con D un dominio limitato. Eseguiamo quindi una decomposizione: