Limite di (e^x-e^-x-2x)/(x-sinx) per x che tende a zero

mercoledì, Febbraio 10th, 2021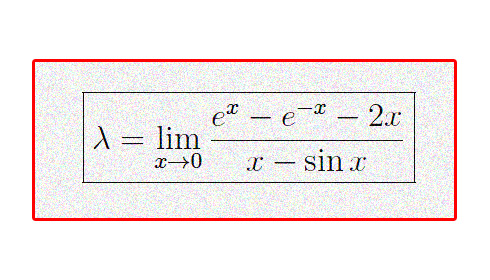

limite per x che tende a zero,esponenziale,sin
Fig. 1

Per calcolre il limite scritto in fig. 1, proviamo a sostituire il valore x=0 e come c'era da aspettarsi esce fuori la forma indeterminata 0/0. Proviamo a vedere se è possibile una qualche manipolazione. A denominatore abbiamo x-sinx, la cui derivata è 1-cosx che ci ricorda un limite fondamentale (quale?). Allora applichiamo la regola di L'Hospital e ovviamente si ripresenta la stessa forma indeterminata. Ma non applichiamo nuovamente L'Hospital bensì un artificio che ci riconduce al predetto limite fondamentale, dopodiché il risultato è quasi immediato.

Scarica l'esercizio in pdf
(altro…)



Posted in Analisi Matematica I | No Comments »