[¯|¯] Oscillazioni forzate. Risonanza
mercoledì, Marzo 22nd, 2017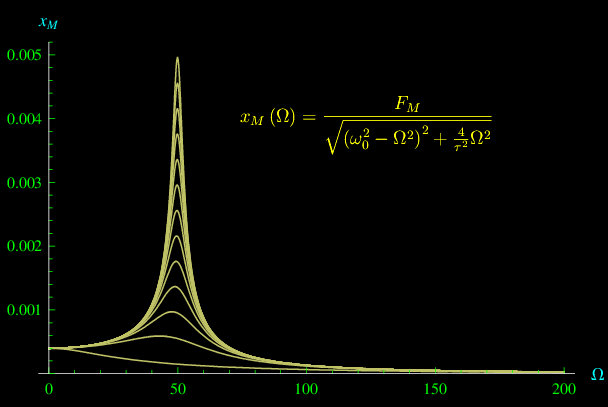
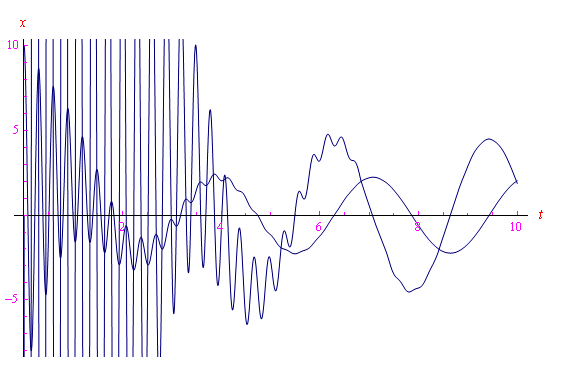
Fig. 1. Ascissa di un oscillatore smorzato sottoposto a una forza funzione sinusoidale del tempo
Abbiamo studiato le oscillazioni forzate in condizioni di idealità, ovvero trascurando le forze di attrito. Nel caso di una sollecitazione esterna funzione sinusoidale del tempo, abbiamo stabilito che se la sua frequenza Ω è di poco inferiore alla frequenza caratteristica ω0 dell'oscillatore, si verifica il fenomeno dei battimenti (che è una conseguenza delle formule di prostaferesi). In particolare, se Ω=ω0 si un battimento di frequenza nulla, ovvero il fenomeno della risonanza.
Consideriamo ora uno scenario più realistico: una forza esterna che sia funzione sinusoidale del tempo, applicata a un oscillatore armonico in presenza di forze viscose. Precisamente:
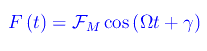
Il secondo principio della dinamica restituisce:
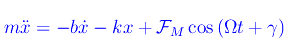
Dividendo primo e secondo membro per la massa m:
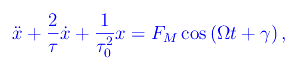
dove
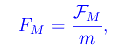
mentre τ e τ0 sono le costanti di tempo introdotte in un post precedente, cioè
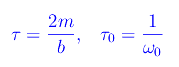
Abbiamo così ottenuto un'equazione differenziale ordinaria del secondo ordine lineare non omogenea. Dalla teoria delle equazioni differenziali sappiamo che il suo integrale generale è:
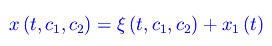
(altro…)

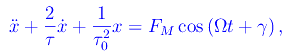
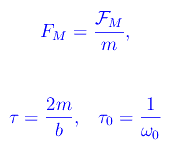
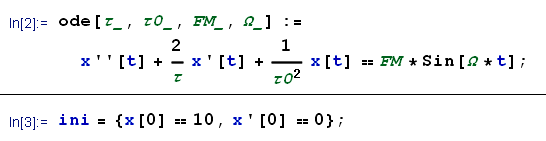



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











