Quadrilatero ciclico e formula di Erone

giovedì, Maggio 27th, 2021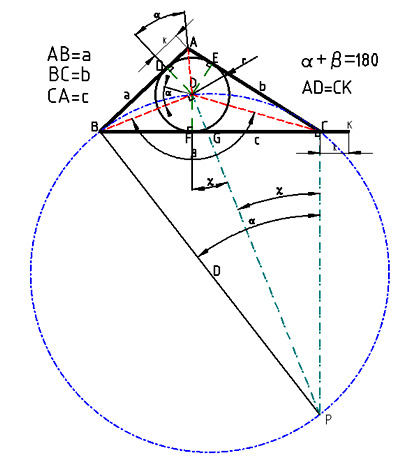

quadrilatero ciclico,formula di erone — **Fig. 1**

Appunti ed esercizi di Geometria elaborati dell'ing. Giorgio Bertucelli.

Si faccia riferimento alla fig. 1, dove è raffigurato un triangolo ABC di cui si conoscano i lati a,b,c. Denominando con p il perimetro p=a+b+c, con s il semiperimetro e con A l'area del triangolo, si vuole dimostrare la formula di Erone:

Soluzione

Si traccino le tre bisettrici per ottenere il centro del cerchio inscritto nel triangolo. I punti di tangenza sono D,E,F. Si estenda il lato BC di un segmento pari a k=AD. Si costruiscano i triangoli BOP e BCP; si potrà dire che essi definiscono il
il quadrilatero ciclico BOCP il cui cerchio (blu) ha il diametro D=BP. Ne segue che l'angolo

è supplementare a

(altro…)

Posted in Geometria | No Comments »

Costruzione di un quadrilatero ciclico

mercoledì, Maggio 26th, 2021

Appunti ed esercizi di Geometria elaborati dell'ing. Giorgio Bertucelli.

Sia dato un quadrilatero ABCD (nero, fig. 1). Si traccino le bisettrici da ciascun vertice prolungandole fino a formare un nuovo quadrilatero EFGH (rosso). Questo si chiamerà quadrilatero ciclico perché risulterà inscritto in un cerchio (blu).