Questa famiglia non ha inviluppo
domenica, Dicembre 27th, 2020
Esercizio
Studiare la famiglia di curve piane:

Soluzione
Osserviamo innanzitutto che la generica curva γλ della famiglia assegnata è il grafico della funzione

data dal prodotto della funzione potenza di esponente reale per la funzione esponenziale e^{-x}. Dobbiamo considerare l'intervallo [0,+oo).
Intersezione con gli assi
Dal momento che l'esponente è maggiore di zero, si ha:

Cioè, il grafico passa per l'origine. Più precisamente, "parte" dall'origine.
Segno
Dal momento che la funzione è definita per x > = 0 ed è ivi non negativa, il grafico è contenuto nel primo quadrante.
Comportamento all'infinito
La funzione è manifestamente infinitesima:

Quindi l'asse x è asintoto orizzontale (a destra).
Derivata prima
Calcolando si trova

Riesce

cosicché la funzione è strettamente crescente in (0,λ) e strettamente decrescente in (λ,+oo). Ne segue che x=λ è punto di massimo relativo, anzi assoluto.

Stabiliamo il comportamento della derivata prima in un intorno destro di x=0. A tale scopo calcoliamo:


Ne segue

Cioè il grafico può "partire" da (0,0) con: 1) tangente verticale; 2) tangente orizzontale ; 3) tangente con coefficiente angolare 1, come illustrato in fig.

Derivata seconda
Abbiamo:

Bisogna però tener conto del fatto che la funzione non è definita per x < 0. Infatti, per 0 < &lmbda; < 1 è x1 < 0, per cui deve essere verificata solo x > x2. Vediamo che x2 è un flesso discendente e che il grafico è convesso in (0,x2) e concavo in (x2,+oo), come vediamo in fig.



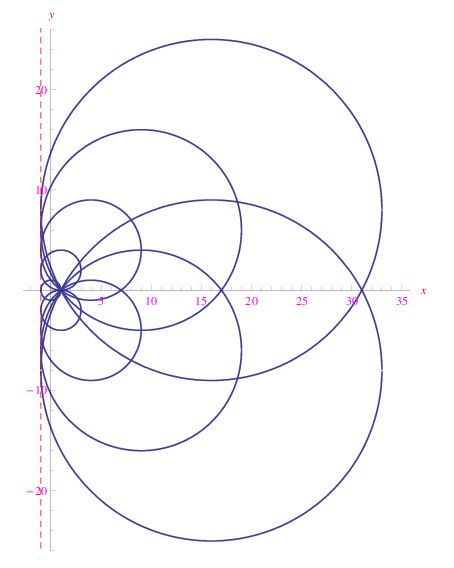
Studiamo le intersezioni delle curve per differenti valori del parametro.

Cioè le curve della famiglia si interesecano nell'origine e in P0(1,(1/e)). Sono questi i punti base della famiglia. Ciò può essere visto applicando il procedimento standard:

Dobbiamo risolvere il sistema:

La prima implica x=0, mentre la seconda y=e^-1, cioè i punti base. Ne concludiamo che la famiglia assegnata non ammette curva inviluppo. In fig. 1 l'andamento di alcune curve della famiglia, in cui sono visibili i punti base.



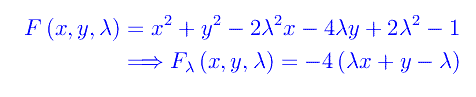
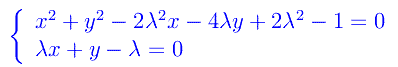



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











