[Studio della funzione] La funzione [1/x]

lunedì, Febbraio 22nd, 2016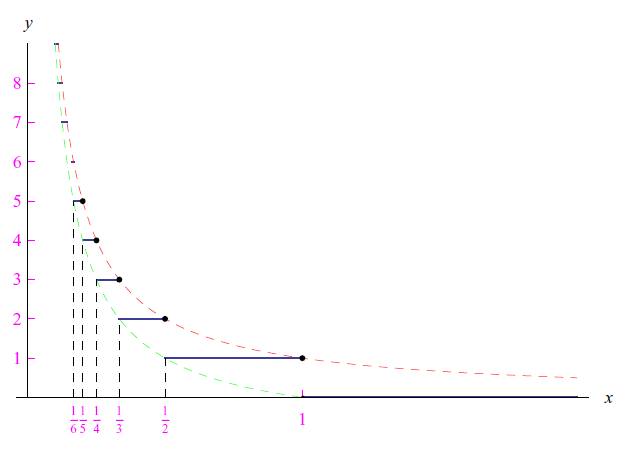

funzione parte intera,punti di discontinuità di prima specie

Nel post precedente abbiamo classificato i punti di discontinuità di 1/[x]. Ora consideriamo la funzione [1/x]. Sembrano uguali (rozzamente parlando; in realtà c'è una bella differenza. Anzi, un universo di mezzo :). Infatti, il grafico di [1/x] si compone di un numero infinito di segmenti di lunghezza decrescente. Più precisamente, la funzione è identicamente nulla in (1,+oo), mentre in (0,1) ritroviamo i suddetti segmenti limitati tra i due rami di iperboli: y=1/x e y=(x-1)/x, come mostrato in figura.

(altro…)

Posted in Analisi Matematica I | No Comments »

Classificazione dei punti di discontinuità di una funzione reale di una variabile reale

sabato, Febbraio 20th, 2016

punti di discontinuità di prima specie,singolarità,discontinuità eliminabili

Nell'handbook precedente abbiamo visto la definizione di funzione continua (di una variabile reale). Esaminiamo ora la classificazione dei punti di discontinuità, ovvero di tutti e soli i punti in cui è violata la predetta definizione.
(altro…)