[¯|¯] Prodotto scalare
sabato, Maggio 26th, 2018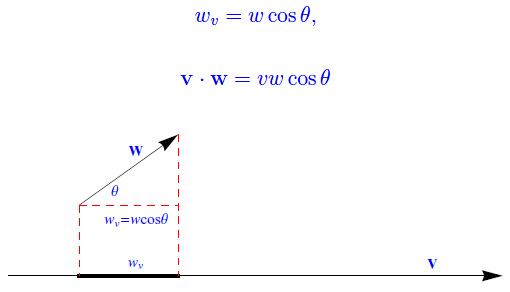
La nozione di componente di un vettore secondo uno dei tre assi coordinati esaminata nella lezione precedente , si generalizza immediatamente: assegnati due vettori v e w, possiamo considerare la componente di w secondo la direzione di v ovvero la proiezione ortogonale di w su v. Denotando con wv tale componente, sussiste la seguente definizione:
Definizione
Il prodotto scalare dei vettori v e w, è dato da vwv, cioè dal prodotto del modulo di v per la componente wv di w secondo la direzione di v.
Il prodotto scalare si denota con v·w:
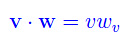
Dalla fig. 1 segue
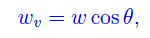
onde
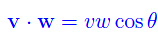
Osservazione
Il prodotto scalare non dipende dal riferimento cartesiano, ma esclusivamente dai vettori considerati.
Per come il prodotto scalare viene definito, segue necessariamente che verifica la proprietà commutativa:
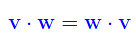
È verificata inoltre, la proprietà distributiva rispetto all'addizione di vettori:
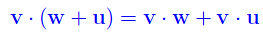
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











