Principio Di Conservazione Del Momento Della Quantità Di Moto |

Moto di un tuffatore (conservazione del momento angolare)

sabato, Febbraio 27th, 2021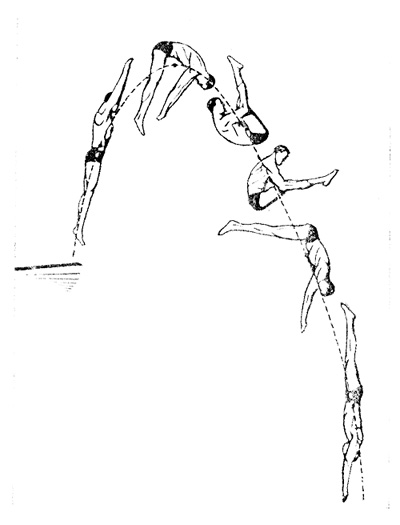

Principio di conservazione del momento della quantità di moto, conservazione del momento angolare, tuffatore — **Fig. 1**

Riprendiamo l'equazione che esprime il momento della quantità di moto di un sistema di punti materiali, in funzione della velocità angolare attorno a un asse per un punto fisso o per il centro di massa, e del momento di inerzia rispetto al medesimo asse:

Si ricordi che tale relazione è valida se tutti i punti del sistema ruotano attorno allo stesso asse e con la stessa velocità angolare. L'equazione si estende ai sistemi continui nelle ipotesi di cui sopra.
Ciò premesso, un tuffatore T (fig. 1) lascia la pedana di lancio con il corpo disteso lungo la verticale.
Il distacco dalla pedana conferisce a T un impulso lineare dp verso l'alto, e un impulso angolare dL tale da determinare una rotazione di T intorno a un asse passante per il centro di massa CM di T. Abbiamo, dunque, un momento della quantità di moto (o momento angolare) L=Iω dove ω è il vettore velocità angolare, mentre I è il momento di inerzia di T rispetto al predetto asse. Si suppone che la velocità angolare sia tale da far compiere a T una rotazione di 180° prima di entrare in acqua. Trascurando la resistenza dell'aria, l'unica forza esterna agente su T è il suo peso P=mg, dove m è la massa di T. Siccome il vettore P è applicato al centro di massa, il momento rispetto a tale punto è nullo (in quanto r=0). Ciò implica che il moto di T conserva il momento angolare:

Osserviamo peraltro che il momento d'ìnerzia è costante solo se T rimane in posizione distesa. Se invece, è in posizione "carpiata" come in fig.1 (ovvero T piega il corpo), il momento d'inerzia diminuisce e conseguentemente aumenta il modulo della velocità angolare in modo che il prodotto rimanga costante. Tale circostanza permette a T di compiere una rotazione maggiore di 180° prima di entrare in acqua.

(altro…)

Posted in Fisica generale 1 | No Comments »

Principio di conservazione del momento della quantità di moto

venerdì, Febbraio 26th, 2021

Il Principio di conservazione del momento della quantità di moto è un caso particolare del teorema della quantità di moto per un sistema di punti materiali. Infatti, si ricava facilmente: se il momento risultante delle forze esterne applicate al sistema, calcolato rispetto a un punto fisso o al centro di massa, è il vettore nullo, il momento della quantità di moto del sistema rispetto al medesimo punto è costante.
Abbiamo ricavato tale principio nel paradigma della meccanica newtoniana. In realtà, si tratta di un principio primo della fisica, valido anche al di fuori del predetto paradigma (meccanica relativistica, meccanica quantistica).

Scarica la lezione in pdf
(altro…)