[¯|¯] Classical bouncing ball: l'accelerazione è un pettine di Dirac

lunedì, Aprile 22nd, 2019

classical bouncing ball, pettine di dirac,accelerazione

In questo hand-book risolviamo il problema del rimbalzo di una pallina da ping pong, lasciata cadere da un'altezza H. Per ora trascuriamo la resistenza dell'aria, integrando l'equazione differenziale del moto con assegnate condizioni iniziali. Vengono fatte particolari ipotesi, nel senso che l'urto pallina-pavimento è considerato elastico, per cui si verifica il fenomeno della riflessione meccanica.
(altro…)



Posted in Fisica generale 1 | No Comments »

[¯|¯] Dirac ha a disposizione infiniti pettini di ordine N

martedì, Febbraio 14th, 2017

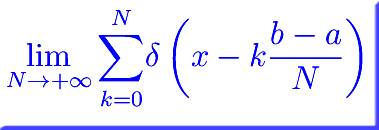
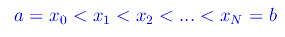
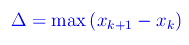
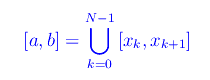
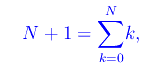
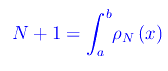
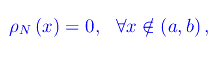
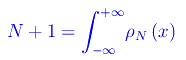
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Eseguiamo una decomposizione D([a,b]) di un intervallo [a,b] contenuto nell'insieme R dei numeri reali, ssegnando ad arbitrio N+1 punti, essendo N un intero naturale non nullo.

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

La norma o ampiezza della decomposizione è il numero reale positivo:

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Segue che [a,b] si decompone in N intervalli:

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Il numero di punti della decomposizione si esprime formalmente

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

dove δ(x-xk) è la funzione delta di Dirac centrata in xk. Quindi

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

Dal momento che

funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

si può scrivere:
funzione delta di dirac,pettine di dirac,teoria delle distribuzioni,punto di accumulazione

(altro…)



Posted in News | No Comments »