Particella vincolata a muoversi sulla superficie interna di un cono

lunedì, Settembre 13th, 2021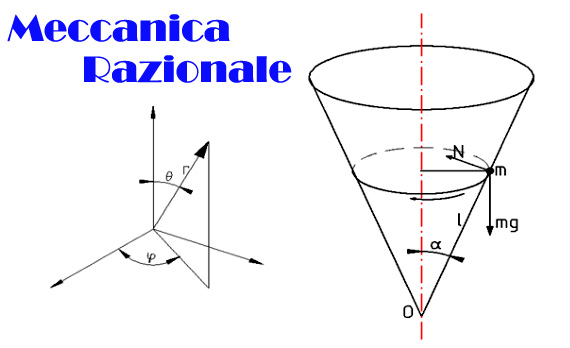

Particella vincolata a muoversi sulla superficie interna di un cono
Fig. 1

Esercizi di Meccanica razionale elaborati dell'ing. Giorgio Bertucelli.

Esercizio

Una particella di massa m è costretta a muoversi, senza attrito, sulla superficie interna di un cono (fig. 1).
a) Trovare le condizioni per cui la particella descrive un'orbita circolare.
b) Verificare la stabilità dell'orbita.

Soluzione

In coordinate sferiche (r,θ,φ) le equazioni del moto sono:


Poiché la particella è costretta a muoversi sulla superficie interna del cono, si ha:

Pertanto la prima delle equazioni del moto si scriverà:

Per il moto in un'orbita circolare attorno al suo asse verticale si ha


Con l=l0 si ha

Essendo

possiamo chiamare

La particella ha una velocità tangenziale v0 all'orbita

Dunque

che è la condizione iniziale che deve essere soddisfatta da v0 e da l0.
(altro…)



Posted in meccanica razionale | No Comments »