Next Entries »

[¯|¯] La funzione esponenziale

lunedì, Dicembre 1st, 2014

funzione esponenziale di base a


Definizione
Assegnato un numero reale a positivo e diverso da 1, dicesi funzione esponenziale di base a, la funzione reale:

funzione esponenziale

La richiesta a diverso da 1 si giustifica osservando che per a = 1 è f(x) = 1, per ogni x. Cioè, la funzione esponenziale di base 1 è la funzione costante f(x) = 1.
Per lo studio della monotonia della funzione esponenziale, prendiamo ad arbitrio e tali che 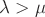, per cui possiamo considerare la funzione potenza di esponente reale positivo:

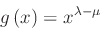
funzione potenza

Per quanto visto nella Lezione 20, la funzione g(x)è strettamente crescente in [0,+oo). Nelle figg. 1-2. riportiamo i casi e tali che .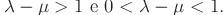

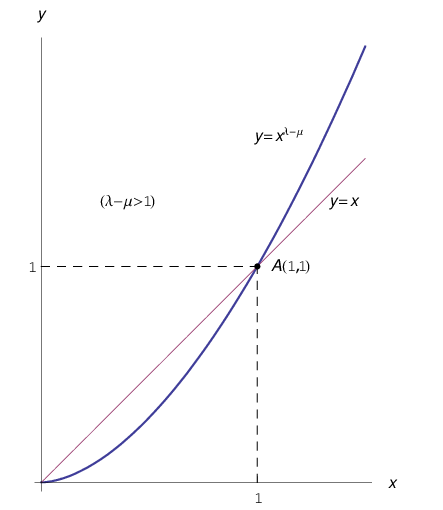
funzione potenza

Fig. 1

funzione potenza

Fig. 2

Caso 1: a >1

Dalla monotonia di g(x) segue:

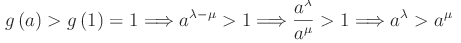
funzione monotona

Cioè:


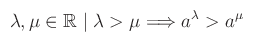
(altro…)



Posted in News | No Comments »

Next Entries »