Spazi di Hilbert. Prodotto hermitiano e metrica

mercoledì, Marzo 10th, 2021

Sia H uno spazio di Hilbert.
Definizione
Comunque prendiamo f,g appartenenti ad H, chiamiamo distanza tra f e g, il numero reale:

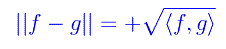
Tale definizione è ben posta in quanto sono soddisfatti gli assiomi che conferiscono alla funzione ρ(f,g) la natura di distanza. Infatti, rammentando le proprietà della norma si ha:

Ne segue che il prodotto hermitiano induce una metrica in H

In altri termini, un qualunque spazio di Hilbert è uno spazio metrico. Ricordiamo incidentalmente, che in topologia una metrica può essere introdotta indipendentemente da un prodotto hermitiano. Di contro, negli spazi di Hilbert la metrica è indotta dal prodotto hermitiano. Alla stessa maniera, in uno spazio euclideo è il prodotto scalare che determina la metrica.
(altro…)

Posted in Analisi Funzionale, Meccanica Quantistica | No Comments »

[¯|¯] Esercizio sugli spazi vettoriali euclidei

venerdì, Maggio 31st, 2019

spazio euclideo,spazio pseudoeuclideo,metrica — **Fig. 1**

Esercizio
Assegnata una base {e_i} di uno spazio vettoriale euclideo 2-dimensionale, il cui tensore metrico ha la matrice rappresentativa nella predetta base, riportata in fig. 1, determinare per quali valori di λ e µ, tale spazio risulta propriamente euclideo.

Soluzione
Abbiamo