Limite di una funzione reale di una variabile reale. Convergenza

giovedì, Febbraio 11th, 2021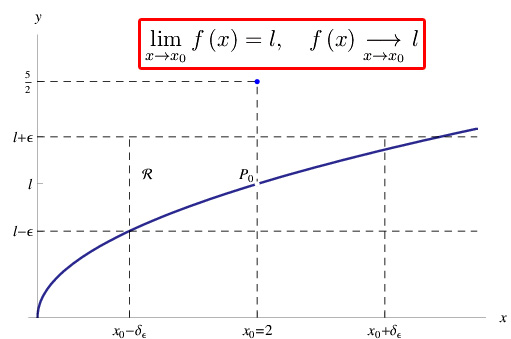

Un esperimento con la calcolatrice

Consideriamo la funzione reale di una variabile reale:

il cui insieme di definizione è X=R-{1}. La funzione è dunque definita su tutto l'asse reale, escluso il punto x0=1. Incidentalmente, se proviamo a calcolare il valore assunto da f in x0, la sua espressione analitica restituisce 0/0 che è una cosiddetta forma indeterminata (o forma di indeterminazione) in quanto l'eventuale risultato dipende dalla funzione considerata. Procuriamoci allora una calcolatrice e andiamo a calcolare i valori assunti dalla funzione in punti prossimi a x0. Ad esempio, per x=1.1, otteniamo:

Avviciniamoci ulteriormente al punto x0:

e così via. Ripetiamo ora lo stesso procedimento per x < 1:

e così via.
Da tali risultati si deduce che possiamo rendere arbitrariamente piccola la differenza |f(x)-2| a patto di avvicinarci sufficientemente a x0=1.

(altro…)