Famiglia di parabole inviluppata dagli assi coordinati

mercoledì, Dicembre 23rd, 2020

inviluppo di una famiglia di curve piane — **Fig. 1**

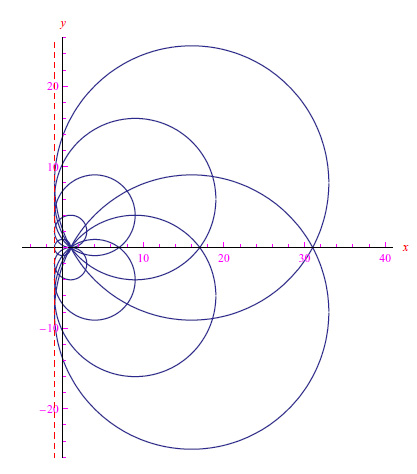
In tutti gli esercizi svolti fino a questo momento, ci siamo concentrati sulla ricerca delle soluzioni del sistema di equazioni che conducono a una qualche rappresentazione parametrica dell'inviluppo di una famiglia di curve piane. Ma non sempre i risultati raggiunti sono così immediati ed è facile confondersi, perché anziché trovare l'inviluppo si determina il luogo dei punti singolari come visto nell'esercizio precedente. Bisogna allora studiare l'eventuale presenza di punti singolari. L'esempio che proponiamo è ancora più suggestivo, in quanto contiene un punto singolare con sorpresa finale: l'inviluppo è l'unione degli assi coordinati.

Scarica l'esercizio svolto in formato pdf
(altro…)

Posted in Geometria differenziale | No Comments »

Inviluppo di una famiglia di curve piane (Envelope of a family of plane curves)

domenica, Dicembre 20th, 2020

Dopo aver introdotto l'evoluta e l'evolvente in teoria delle curve piane, passiamo alla definizione di curva inviluppo di una famiglia di curve piane regolari. Dal nome si intuisce che si tratta di una curva tale che in ogni suo punto passa una ed una sola curva della famiglia che risulta ivi tangente all'inviluppo.
La ricerca dell'inviluppo non è semplice in quanto richiede l'applicazione del teorema del Dini esteso a un sistema di due equazioni. Rilassando le condizioni di regolarità del predetto teorema si perviene all'esistenza di soluzioni improprie geometricamente denominate punti base della famiglia assegnata.

Scarica la soluzione in pdf

(altro…)