[¯|¯] Applicazioni tra insiemi

venerdì, Giugno 8th, 2018

Siano S ed S' due insiemi non vuoti.
Definizione
Dicesi applicazione o funzione di S in S' una legge che associa ad ogni elemento x di S un elemento x' di S'. Un'applicazione è simboleggiata da una delle seguenti notazioni:

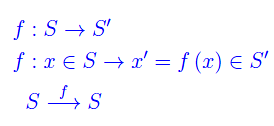
L'elemento x'=f(x) si chiama immagine di x mediante f. Il sottoinsieme di S'

si chiama immagine di S mediante f. Per un assegnato x' di S', il sottoinsieme di S:

si dice controimmagine di x' mediante f. Tale sottoinsieme è vuoto se e solo se x' non appartiene a f(S):

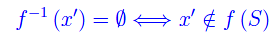
Definizione
Le applicazioni f:S->S' e g:S->S' si dicono coincidenti e si scrive f=g, se

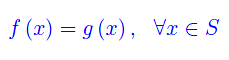
Esempio 1
Assegnata ad arbitrio una retta r di un piano α, consideriamo l'applicazione che a ogni punto di α associa il punto P' dato dall'intersezione di r con la retta r' per P e ortogonale a r, come mostrato in
fig.

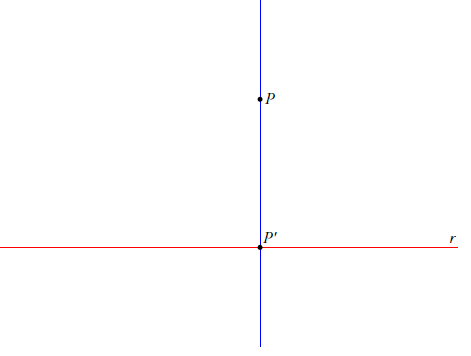
Quindi

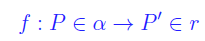
Riesce

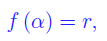
cioè l'immagine di α mediante f è la retta r. Per un assegnato P' di r:

ovvero la controimmagine di un un generico P'di r è la retta r'.

Esempio 2
In un piano α consideriamo due rette parallele r ed r'. Sia O un punto appartenente al semipiano delimitato inferiormente da r, come mostrato nella figura al top di questa pagina, dove è riportato testo e risultati.

Sostienici

Vai alla lezione successiva

Vai alla lezione precedente

Indice delle lezioni

Posted in Algebra | No Comments »

[¯|¯] Esempio di corrispondenza tra insiemi

lunedì, Giugno 4th, 2018

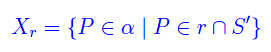
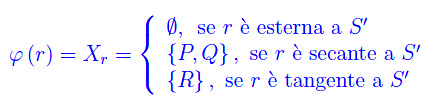
corrispondenza tra insiemi,insieme delle parti,immagine,antimmagine — **Fig.1**

Vediamo un esempio di corrispondenza tra insiemi

Assegnato un piano α dello spazio ordinario, denotiamo con S l'insieme delle rette contenute in α, e una circonferenza di tale piano, quale insieme S' di punti di α equidistanti da un punto assegnato (centro della circonferenza).

Comunque prendiamo una retta r di S, l'insieme dei punti di intersezione di r con S' è un sottoinsieme di S', i.e. un elemento dell'insieme delle parti di S' che solitamente si indica con P(S'). Indichiamo con Xzsub>r l'insieme dei punti in comune tra un'assegnata retta r e la circonferenza S'. Cioè

Nel caso della fig. 1:
corrispondenza tra insiemi,insieme delle parti,immagine,antimmagine

Infatti le tre rette r₁,r₂,r₁ sono rispettivamente esterna, secante e tangente alla circonferenza S'. Possiamo, quindi, stabilire una legge che associa a ogni retta di α un insieme di punti di S'. Tale legge è manifestamente una corrispondenza da S verso S':

Per quanto precede:

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Vai alla lezione successiva

Vai alla lezione precedente

Indice delle lezioni