[¯|¯] Proprietà della relazione di inclusione. Insieme delle parti
Giugno 7th, 2018 | by Marcello Colozzo |
Nella lezione precedente abbiamo definito l'inclusione di un insieme A in un insieme B:

Comunque prendiamo un insieme A, la relazione di inclusione verifica le seguenti proprietà:
- Proprietà riflessiva

cioè A è contenuto in sé stesso. - Proprietà antisimmetrica

- Proprietà transitiva
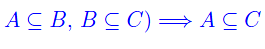
Insieme delle parti

Definizione
Comunque prendiamo un insieme S, dicesi insieme delle parti di S, l'insieme
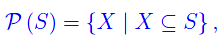
cioè l'insieme i cui elementi sono tutti e soli i sottoinsiemi di S.
In altri termini, assegnato un qualunque insieme S, i suoi sottoinsiemi pensati come elementi, costituiscono l'insieme delle parti di S.
Proposizione

Dimostrazione
L'asserto discende da una proprietà esaminata in precedenza, e cioè
per cui P(S) contiene almeno un elemento. Più precisamente
Proposizione
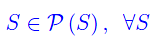
Dimostrazione
Comunque prendiamo S:
Proposizione
Se S è costituito da n elementi distinti, P(S) è costituito da 2n elementi distinti.
Dimostrazione
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)Articoli correlati

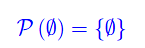

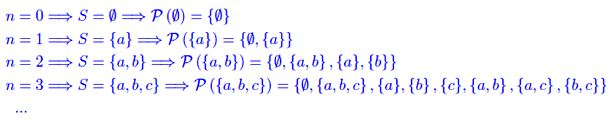


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











