[¯|¯] PNT - Teorema dei Numeri Primi
mercoledì, Febbraio 14th, 2018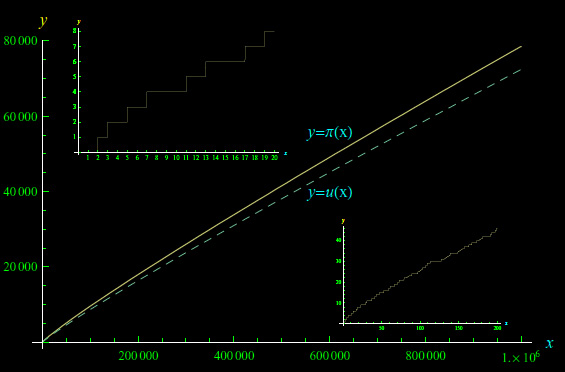
In fig. 1 riportiamo il grafico della funzione di distribuzione dei numeri primi (generato con Mathematica) confrontato con la sua approssimazione asintotica u(x)=x/ln(x) in virtù del Teorema dei Numeri Primi. Tale approssimazione oltre a essere asintotica, è non-locale i.e. globale, giacché non riproduce le discontinuità locali della funzione di distribuzione dei primi. Per quanto visto, le predette discontinuità (in corrispondenza dei numeri primi) sono generate dalla distribuzione degli zeri non banali della funzione zeta di Riemann. Incidentalmente, la parte reale e la parte immaginaria della zeta sono funzioni rapidamente oscillanti (in particolare sulla linea critica).
(altro…)

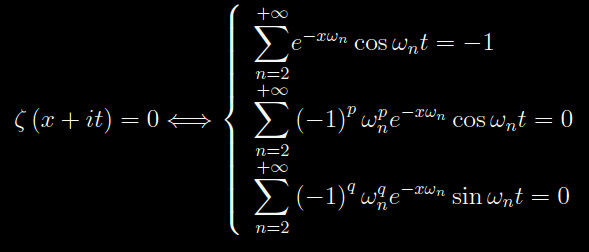


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











