[¯|¯] La funzione logaritmo

mercoledì, Dicembre 3rd, 2014

Oggi introduciamo un'importante funzione elementare: la funzione logaritmo. Nello studio della funzione esponenziale abbiamo:

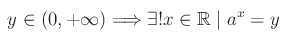
per cui l'equazione:
equazione esponenziale

è compatibile e determinata, i.e. ammette una ed una sola soluzione.

Definizione
Per y>0 l'unica soluzione della suddetta equazione dicesi logaritmo di y in base a, e si indica con il simbolo:

Cioè:

Risolvere l'equazione assegnata equivale a determinare la funzione inversa di
Per quanto visto nella precedente, è strettamente monotona, per cui è invertibile:

onde:

Per la conservazione della monotonia della funzione inversa si ha che per a >1 la funzione

è strettamente crescente. Per 0<a<1 è strettamente decrescente. In entrambi i casi il codominio è (-oo,+oo).
Studiamo il segno della

. Iniziamo con l'osservare che

. Infatti:
logaritmo di 1

(altro…)

Posted in Analisi Matematica I | No Comments »

[¯|¯] Esercizio sulle funzioni inverse (parte 2)

lunedì, Ottobre 6th, 2014

Studiare l'invertibilità della funzione:

Svolgimento
Il campo di esistenza della funzione assegnata è il campo reale. Il suo grafico è la parabola y=x^2 ed è facile convincersi che la funzione non è strettamente monotona, onde non invertibile. Però è localmente monotona in senso stretto. Precisamente, risulta strettamente crescente in A=[0,+oo) e strettamente decrescente in B=(-oo,0].
(altro…)